本資料は,東北大学工学部機械知能・航空工学科 4年生向け講義「信号処理工学」(2013年度までは「知能情報システム工学」)の補足資料とすることを意図したものです.「やる夫」と「やらない夫」という2人の架空の人物の会話形式でディジタル信号処理工学の基本的な部分を説明することを狙います.
ただし,いわゆるディジタル信号処理の講義とは少し力点が異なっている面があります.それは以下のような状況に起因します.
- 同講義の受講者は,原則として3年生の時点で「数学II」としてフーリエ解析・ラプラス変換を,「制御工学I」「制御工学II」として古典・現代制御論を履修している.
- 同講義は4年生の前期の開講であり,多くの受講者にとっては大学院入試の直前の時期の受講になる.
- 東北大学機械系の大学院に進学する場合,数学II,制御工学I・II は院試の科目として必要となる受講者が多い.一方,ディジタル信号処理は院試の範囲外である.
これらを考慮して,同講義 (およびこの補足資料) では,ディジタル信号処理の技術自体を学んでもらうことよりも,ディジタル信号処理というネタを通じて,フーリエ解析,ラプラス変換,線形システム論,制御論などについて復習し,理解を深めてもらうことに主眼をおくことにしています.
この点を反映して,本資料の生徒役である「やる夫」は,講義の受講生と同様に,フーリエ解析,ラプラス変換,制御工学等は一通り学んだことがある (はずである) が,いまいち理解し切れていない人物として描かれています (が,もちろんこれらの初学者でも理解できるように書いているつもりです).教師役である「やらない夫」が何者なのかは,書いてる自分でもよくわかりません.
本資料は2011年前期セメスターの講義を進めながら執筆・都度公開し,予定していた内容を同年8月までに一通り書き上げました.今後も適宜更新していく予定です.
執筆に当たっては,講義で教科書として指定している 樋口・川又(2000) を構成も含めて大いに参考にしているほか,下記の各文献を主に参照しています.
- 樋口 龍雄, 川又 政征: ディジタル信号処理 ― MATLAB対応, 昭晃堂, 2000.
- Alan V. Oppenheim and Ronals W. Schafer:
Discrete-time Signal Processing, Prentice Hall, 1998.
- 眞渓 歩: ディジタル信号処理工学, 昭晃堂, 2004.
- H. P. スウ著, 佐藤 平八 訳: フーリエ解析, 森北出版, 1979.
この資料はいわゆる やる夫シリーズ
の体裁を借りたものですが,同シリーズに特徴的なアスキーアートによる挿絵はありません.これは権利上の問題を避けるためと同時に面倒くさいためですが,圧倒的に後者の事情が大きいです.挿絵を独自に追加したバージョンを作成されるのは,特に止めませんが,推奨もしません.
2011年10月頃から,
twitter
や
はてなブックマーク
等で多数言及されるようになり,予想以上の反響に驚いています.大変ありがたいことなのですが,ツイートやコメントを読んでいると「普通の信号処理の教科書の語尾を『だお』に変えただけのもの」を公開していると思われている節が (一部に) あるようです.
もちろんそんな酔狂なことに時間を割いているはずはなく,わざわざ新しいテキストを書き起こしたのにはそれなりの意図があります.基本的には,数式の背後にある概念やそのとらえ方を,できるだけ嘘のない形で伝えることを試みました.そのために
- 新しい概念や定義を導入する際,なぜそれが必要なのかを可能な限り説明する
- 数式を展開して証明終わり,ではなく,できるだけ直観的な説明をする.数式の展開が必要な場合は,その式変形の意図をできるだけ説明する
ことを心がけました.そのような書き方のためには,わからないことを遠慮なく「わからない」と言う,やる夫のような生徒役との会話形式が適していると考えました.
以下,各章の特色だと思うところ (普通の教科書と,どこが同じでどこが違うのか) を挙げます.当該分野について一通り学習したことのある方にとっては,どの章を読み飛ばしてどの章を読めばよいかを判断するための材料になるのではないかと思います.
- 1. フーリエ級数
- 理工系向けの教科書としてはごく一般的な導入方法を踏襲している.つまり,周期関数を三角関数系で展開「できるとしたら」こういう形にしかなり得ない,という議論でフーリエ級数展開を導いている.初学者向けにはこれが一番わかりやすい議論だと思っているが,数学書は普通こういう流れでは書かれていない.なぜ理工書と数学書でこうも違うのかを 2.4節で説明することにした.
- 2. 複素指数関数型のフーリエ級数
- フーリエ級数をまず三角関数系で導入して,それから指数関数系で表示し直すのも常道を踏襲している.ただし,式変形で導出して終わりではなく,振幅と位相の明示的な表示になっていることを強調した.また,指数関数型にすることで現れる「負の周波数」の意味するところを明示した.
- 3. フーリエ変換
- フーリエ級数から極限操作によって導入しており,これも標準的なやり方と思われる.ただし極限への移行の過程はちょっとくど過ぎるかもしれないくらい丁寧に描出した (わかっている人にとっては鬱陶しいだけだと思う).フーリエ変換対の計算例は,以降の議論で必要になるものに限定した.また,これも後々の議論のため,周期関数を (フーリエ級数展開ではなく) フーリエ変換するとデルタ関数の列が出てくることを説明しておくことにした.
- 4. 離散時間信号
- この章は標準的な説明に終始している.正規化周波数の概念と,離散時間の複素指数関数が周波数に関して周期的であることを説明している.
- 5. 離散時間フーリエ変換
- フーリエ変換の時間領域を離散化することで離散時間フーリエ変換を導出している.それ自体は標準的なやり方と思われるが,区分求積法的な説明と,デルタ関数を使った説明の両方を併記した.そして,後者からの流れで4章で張った伏線を回収し,フーリエ級数と離散時間フーリエ変換が,時間と周波数を逆にした関係にあることを強調することにした.
- 6. 離散フーリエ変換
- 離散フーリエ変換は,離散時間フーリエ変換の周波数領域の離散化からでも,フーリエ級数の時間領域の離散化からでも導入できるが,前の章とのつながりがよいので前者によることにした.これで時間・周波数領域それぞれの連続・離散の4組み合わせが出揃ったので,その対称性について改めて見渡しておくことにした.高速フーリエ変換のアルゴリズムは,とりあえず以降の議論のためには知らなくても差し支えないことと,標準的な説明以上のことが思いつかないことにより,そういう便利なものがあるということだけ述べておくに留めた.
- 7. フーリエ変換の性質(1): 時間シフトと変調
- フーリエ変換にはいくつか重要な性質があるが,連続・離散に関する4種類のフーリエ変換について同様に成り立つため,まとめて並べて示すことにした.いずれも,多くの教科書では数式の展開により証明していることが多いが,それは敢えて避けて,直観的に説明することを試みた.時間シフト (と変調) については,周波数成分ごとの時間シフトの観点で説明している.
- 8. フーリエ変換の性質(2): たたみこみと積
- たたみこみと積の関係は,フーリエ変換の性質のうちでも特に利用頻度の高いものだが,(数式の展開による証明で済まさず) 直観的に理解しておこうとするなら,線形時不変システムの概念が必須であると思う.ちょっと遠回りになるが,線形時不変システムの作用としてたたみこみを説明し,周波数応答の概念を用いてたたみこみと積の関係を説明した.遠回りと言っても,後のディジタルフィルタの理解のためにはどうせ必要になる概念なので,無駄足ではない.
- 9. フーリエ変換の性質(3): パーセバルの等式
- フーリエ変換をある種の正規直交展開として幾何学的に捉えられるようになっておくことは,さまざまな概念の直観的な理解のために重要である.問題はそれをどこで導入するかだが,パーセバルの等式を説明する際にやっておくことにした.幾何学的に捉えてしまえば,パーセバルの等式はいわゆるピタゴラスの定理みたいなものであり,直観的にほとんど当たり前に思えるようになるのだが,実は必ずしも当たり前ではないということは釘を刺しておくことにした.
- 10. サンプリング定理
- サンプリング定理自体は,十分な準備さえできていれば数行の数式展開で証明できる話である.「準備」というのは主に「くし型関数」に関する理解であるが,これをあらかじめ学んでおこうと言ってもご利益がわからないように思うので,サンプリング定理を証明する過程で必要に駆られて出てくる流れにした.くし型関数のフーリエ変換やくし型関数のたたみこみについても,できるだけ直観的な説明を試みた.せっかくくし型関数三昧になったので,4種類のフーリエ変換の関係も,くし型関数を使っておさらいしておくことにした.
- 11. スペクトル解析と窓関数
- 標準的な説明に終始している.読者が「信号にFFTをかけてスペクトル解析をしたい」と思っていてディジタルフィルタには興味がないのであれば,とりあえずここまで読めばOK.
- 12. ディジタルフィルタの基礎
- (線形)ディジタルフィルタとは,すなわち9章で説明した線形時不変システムそのものなわけで,そこが説明済みである以上,FIRフィルタの導入ほとんど自明である.問題はどうやって再帰型IIRフィルタに話を持っていくかだが,樋口・川又(2000) に倣って,一般論ではなく具体例 (実指数関数応答) で導入することにした.
- 13. ラプラス変換
- z変換を理解するにはラプラス変換を理解しなくてはならない.ラプラス変換とは何なのかというと,フーリエ変換する際に元の関数に実指数関数をかけておいて収束しやすくするものなわけだが,そのように説明されたところで,なぜラプラス変換が微分方程式論や線形システム論で便利に使えるのかピンと来ない.それもそのはずで,別に収束しやすくなったから便利に使えるようになったわけではないからだ.この点の説明をちゃんとすることを試みた.
まず,微分方程式が代数方程式に置き換えられる理由を,周波数成分ごとの微分を考えることで説明した.これはフーリエ変換の教科書によく出てくる説明である (つまりこの性質はラプラス変換の専売特許ではないということだ).じゃあ何のためにラプラス変換が必要なのか (なぜ s という新しい変数が必要なのか) という疑問には,伝達関数の極の観点から説明することにした.また,
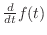 のラプラス変換が
のラプラス変換が 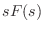 ではなく
ではなく
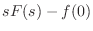 になる理由について直観的な説明を試みた.
になる理由について直観的な説明を試みた.
- 14. z 変換
- 前章でラプラス変換の意義をじっくり説明したので,z 変換も同様の流れを繰り返す形で説明した.
- 15. ディジタルフィルタの解析
- 取り扱っている話題自体は,安定性,線形位相性,群遅延など標準的なものばかりである.それぞれの条件や意味をできるだけ直観的に説明するようにしたが,群遅延の式の導出はあまり直観的とはいえないかも知れない (基本的には Oppenheim & Schafer (1998) の説明そのままである).具体例として用いる関数の大部分は樋口・川又(2000) に倣った.
- 16. ディジタルフィルタの設計
- ほぼ標準的な説明である.
- 2016.01.08
- 小さな修正をいくつか.
- 式 (2.27) で
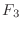 を
を 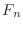 と書いていたのを修正.
と書いていたのを修正.
- sinc 関数が時刻 0 で値 0 を取るかのような書き方になっていた (
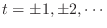 とかに勢い余って 0 を加えていた) のを修正.
とかに勢い余って 0 を加えていた) のを修正.
- フーリエ級数展開を表す FSつきの矢印 の説明が重複していた (説明済みなのにフーリエ変換の章で再度説明していた) のを修正.
- 2014.11.03
- ほぼ一年ぶりの更新.重要な変更点は以下の通り.
- 2013.11.02
- 線形時不変システムとたたみこみについて,連続時間の場合の説明を追加した.また,以前の版では巡回たたみこみ (周期たたみこみ) を表すために普通のたたみこみとは違う記号を導入していたのだけど,結局最後まで使わなかったので削除 (正確には,だいぶ前に削除していたのだが一部残骸が残っていた.今回でおそらく完全に削除).
- 2013.10.27
- ずっと気になっていたのだけど,前書き」に章番号がついて実質的な最初の章 (フーリエ級数) が 2 章から始まるのが気持ち悪かったので思い切って変更.これにより過去の版とは章番号が 1 個ずつずれることになった.過去の更新履歴に書かれている章番号もずれたままなのでご注意ください.
ついでに他にも細々と修正.特に図の見た目 (色使いとか) をいろいろ更新.
- 2013.10.5
- いろいろまとめて更新.大きなものは以下の通り.
- バタワースフィルタの理論を付録として追加.この点が完全に天下りだったのを解消.
- 高速フーリエ変換の説明を付録として追加するかしないかずっと迷っていたのだが,追加しないことにした.やはり月並みな説明以上のことを書けそうにない.7章で「そのうち話す」的なことを書いていた部分を削除.
- 9章: たたみこみと積の関係の連続時間版の導出も書いておくことにした.ラプラス変換目当てで読もうとする方もいるようなので,そのような場合は,フーリエ級数 → フーリエ変換 → フーリエ変換の性質 (特にたたみこみ) → ラプラス変換,と進めば話は一応つながっている,はず.
- 14章: 連続時間の単位ステップ関数の場合分けは,
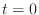 は
は 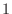 の方に入れる方が一般的なようなので,そちらに修正.
の方に入れる方が一般的なようなので,そちらに修正.
- 2013.05.11
- いくつか説明表現や字句の修正をしたほか,以下のミスを訂正.
- 4章: 「
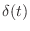 をフーリエ変換したら
をフーリエ変換したら
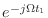 になる」等の
になる」等の 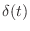 はもちろん「
はもちろん「
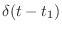 」の誤り.
」の誤り.
- 式(4.44)〜(4.45)の説明図の
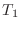 は
は 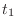 の誤り.
の誤り.
- 2012.08.04
- 以下の図のミスを訂正.
- 7章: 低周波数と高周波数の帯域の説明図で,
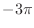 →
→ 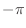 ,
,
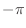 →
→ 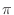 に修正.
に修正.
- 14章: 部分分数展開に対応するブロック図でラベル
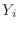 の位置が正しくなかった (重み
の位置が正しくなかった (重み 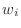 をつけた後になっていた) のを修正.
をつけた後になっていた) のを修正.
- 17章: バタワースフィルタの振幅特性の図で
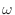 を
を 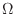 に,
rad を rad/s に修正.
に,
rad を rad/s に修正.
ついでに (最近こればっかり),HTML 版の数式番号等のリンクにマウスポインタを乗せたときに,リンク先の数式等がポップアップするようにしてみた.
…というような説明をここに書いていても誰も読んでいない気がするので,トップページにもう少し情報を集約してみることにした.
- 2012.07.15
- 以下の明らかなミスの他,いくつかの箇所で表現を修正.
- 16章: 「つまり
![$ x[n] = \cos{2\pi n}$](img32.png) とかを入力すると出力は 0 になる」 →
とかを入力すると出力は 0 になる」 →
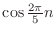 に修正.(
に修正.(
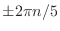 と
と
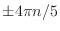 のどれでもよい)
のどれでもよい)
- 17章: バタワースフィルタの定義式で
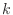 の範囲がずれていたのを修正.
の範囲がずれていたのを修正.
ついでに (どっちがついでだかわからないが),「アスキーアートがない時点で全く読む気が起きない」という読者へのささやかな対応として,
やる夫とやらない夫をそれぞれアイコンで置き換える機能を追加.ページ上部の「アイコンを表示する」をクリックしてください.まあ機械的に置き換えているだけで表情とかは全部同じなので,意味があるかはわかりませんが.アイコンはこちらのサイトから頂きました.
- 2012.07.13
- 誤字・脱字の類をいくつか修正.本年度の講義が進行中
(もう終盤) ですが,受講生から指摘を頂いた脱字も修正しています.ありがとうございました.
それに加えて,ずっと懸案だった付録「伝達関数の部分分数展開」を公開.ラプラス変換や z 変換の章で省略した事項の補足説明になります.
- 2012.01.22
- 文章内の相互参照リンクを設けてみた.「前に出てきたあの話と同じ」的な部分がわかりにくいとの声を頂いたためですが,多少でも緩和できたかどうか.ざっと見直して気づいたところに挿入しただけなので,まだ足りないとは思いますが.
相互参照するに当たっていくつかの箇所で表現を調整したほか,その過程で気づいた以下の各箇所も修正:
- 4.4節: 離散的にしか値を持たない連続信号の積分についての説明を微修正.リーマン積分では定義できないと読み取られる恐れがあったので回避する.(もともとリーマン積分とは書いていないので間違いではないのですが)
- 7.6節: 「マトリックス状に表すとこうなる」と書いておきながら図を入れ忘れていたので追加.(半年以上前に自分で描いた図だが…これはわかりやすいのか?)
- 14.4節: 積分と総和を交換するところが,何かを誤魔化している風の言い回しだったが,別に何の問題もないので修正.
- 14.5節: 極が複素数の場合の説明を追加.最後の「フーリエ変換のまま
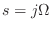 と置いちゃダメなのか?」のところも説明を追加.伝達関数の分解図で
と置いちゃダメなのか?」のところも説明を追加.伝達関数の分解図で 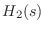 等がなぜか
等がなぜか 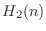 等になっていたのを修正.
等になっていたのを修正.
- 2012.01.16
- 3章: 「
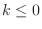 の
の 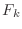 だけわかれば」→「
だけわかれば」→「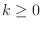 の
の 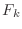 だけわかれば」と,10章の式(10.8)が全く無意味なものになっていた (おそらく作業時のコピー・ペーストミス) のを修正
(以上のミスは Takayoshi Kawada (@takkaw) 様にご指摘頂きました).また,1.2節として各章の執筆意図説明を追加.
だけわかれば」と,10章の式(10.8)が全く無意味なものになっていた (おそらく作業時のコピー・ペーストミス) のを修正
(以上のミスは Takayoshi Kawada (@takkaw) 様にご指摘頂きました).また,1.2節として各章の執筆意図説明を追加.
- 2011.08.18
- 17章「ディジタルフィルタの設計」を公開.一応これで当初予定していた内容は一通り書いたことになるので,PDF版も公開 (トップページ先頭にリンクあり).その他以下のしょうもないミスを修正:
- 11章: 「
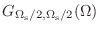 のフーリエ変換」→「
のフーリエ変換」→「
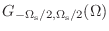 の逆フーリエ変換」
の逆フーリエ変換」
- 14章: 「
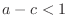 」 → 「
」 → 「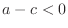 」
」
- 15章:「基本的にはどういうことだが」→「基本的にはそういうことだが」,「離散時間フーリエ変換を
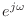 と書く場合がある」→「離散時間フーリエ変換を
と書く場合がある」→「離散時間フーリエ変換を
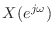 と書く場合がある」
と書く場合がある」
- 2011.08.04
- 16章「ディジタルフィルタの解析」を公開.
- 2011.07.25
- 15章「z 変換」を公開.14章のラプラス変換表の誤りを訂正 (
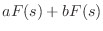 はもちろん
はもちろん
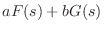 の誤記でした).ついでに15章のまとめとの対応を取るため,
14章のまとめに「時間微分 → s倍」の関係を追加.
の誤記でした).ついでに15章のまとめとの対応を取るため,
14章のまとめに「時間微分 → s倍」の関係を追加.
- 2011.07.16
- 14章「ラプラス変換」を公開.6章の最後で
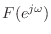 や
や
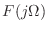 の表記についての言及を減らして,後にラプラス変換や z 変換が出てきたところで説明することにする.
の表記についての言及を減らして,後にラプラス変換や z 変換が出てきたところで説明することにする.
- 2011.07.09
- 13章「ディジタルフィルタの基礎」を公開.
- 2011.07.08
- 12章「スペクトル解析と窓関数」を公開.
- 2011.07.03
- 11章「サンプリング定理)」を公開.HTML版の体裁を (例えば章番号を表示するなど) 微調整.「HTML版の」ということはPDF版も一応の用意はあるということなのですが,需要はあるのでしょうか.
- 2011.06.23
- 10章「フーリエ変換の性質(3)」を公開.
- 2011.06.16
- 8章「フーリエ変換の性質(1)」と9章「フーリエ変換の性質(2)」を公開.
- 2011.06.03
- 1章「前置き」のtypoを修正.「ディジタル信号処理は院試の範囲である」→「ディジタル信号処理は院試の範囲外である」…こ,これはひどい.(院試の出題範囲については,必ず公式情報を確認してください)
- 2011.05.27
- 7章「離散フーリエ変換」までを公開.
- 2011.05.20
- 4章「フーリエ変換」までをとりあえず公開.
swk(at)ic.is.tohoku.ac.jp
2016.01.08
![]() のラプラス変換が
のラプラス変換が ![]() ではなく
ではなく
![]() になる理由について直観的な説明を試みた.
になる理由について直観的な説明を試みた.