: 7. フーリエ変換の性質(1): 時間シフトと変調 : やる夫で学ぶディジタル信号処理 : 5. 離散時間フーリエ変換 目次 アイコンを表示する
周期的でない離散時間信号の場合,離散時間フーリエ変換することで,周期
![]() で,連続的なスペクトルが得られるんだった.
で,連続的なスペクトルが得られるんだった.
![\includegraphics[scale=0.5]{fig_dft/dtft_aperiodic.eps}](img463.png)
これが,![]() が周期的な場合にどうなるかを考えてみるわけだ.まず,スペクトル
が周期的な場合にどうなるかを考えてみるわけだ.まず,スペクトル ![]() が離散的になるってのは,これまで話して来た通りだ.じゃあ,各点の
が離散的になるってのは,これまで話して来た通りだ.じゃあ,各点の ![]() はどういう値になるか?
はどういう値になるか?
![\includegraphics[scale=0.5]{fig_dft/dtft_periodic.eps}](img464.png)
で,逆変換である ![]() の計算の方は
の計算の方は ![]() を積分するわけだが,
を積分するわけだが,
![]() の間隔でデルタ関数が並んだ
の間隔でデルタ関数が並んだ ![]() を長さ
を長さ ![]() の区間で積分するわけなので,要するにインパルス
の区間で積分するわけなので,要するにインパルス ![]() 本の面積を足し合わせることになるわけだ.それによって,元の有限値の列
本の面積を足し合わせることになるわけだ.それによって,元の有限値の列 ![]() に戻るという仕組みだ.
に戻るという仕組みだ.
まずは,![]() をこんな風に表すところから始める.
をこんな風に表すところから始める.
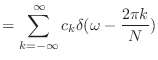 |
(6.1) |
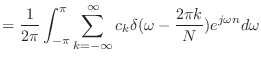 |
(6.2) | |
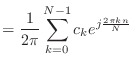 |
(6.3) |
![$\displaystyle = \sum_{n = -\infty}^{\infty} f[n] e^{-j\omega n}$](img427.png) |
(5.3) |
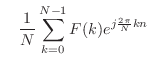 |
(6.6) | |
![$\displaystyle = \frac{1}{N} \sum_{k=0}^{N-1} \left[ \sum_{m=0}^{N-1} f(m) e^{-j \frac{2\pi}{N} km} \right] e^{j\frac{2\pi}{N} kn}$](img483.png) |
(6.7) | |
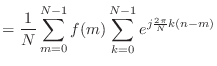 |
(6.8) | |
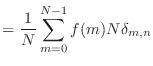 |
(6.9) | |
| (6.10) |
![\includegraphics[scale=0.5]{fig_dft/dft_periodic.eps}](img487.png)
まとめよう.
![\includegraphics[scale=0.5]{fig_dft/dft_freq_dist.eps}](img494.png)
| (6.11) | ||
| (6.12) | ||
| (6.13) | ||
| (6.14) | ||
| (6.15) |
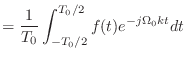 |
フーリエ係数の計算 | (2.28) | ||
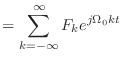 |
フーリエ級数 | (2.18) | ||
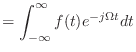 |
フーリエ変換 | (3.11) | ||
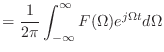 |
フーリエ逆変換 | (3.10) | ||
![$\displaystyle = \sum_{n = -\infty}^{\infty} f[n] e^{-j\omega n}$](img427.png) |
離散時間フーリエ変換 | (5.3) | ||
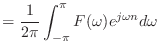 |
離散時間フーリエ逆変換 | (5.8) | ||
![$\displaystyle = \sum_{n = 0}^{N-1} f[n] e^{-j \frac{2\pi}{N}kn}$](img508.png) |
離散フーリエ変換 | (6.5) | ||
![$\displaystyle = \frac{1}{N} \sum_{k = 0}^{N-1} F[k] e^{j\frac{2\pi}{N} kn}$](img509.png) |
離散フーリエ逆変換 | (6.4) |
離散性と周期性に注目して表にするとこんな感じになる.
| 時間領域 | 周波数領域 | |||
| 離散性 | 周期性 | 離散性 | 周期性 | |
| 連続 | 周期的 | フーリエ級数展開
|
離散的 | 非周期的 |
| 連続 | 非周期的 | フーリエ変換
|
連続 | 非周期的 |
| 離散的 | 非周期的 | 離散時間フーリエ変換
|
連続 | 周期的 |
| 離散的 | 周期的 | 離散フーリエ変換
|
離散的 | 周期的 |
![\includegraphics[scale=0.5]{fig_dft/periodic_discrete_matrix.eps}](img512.png)
フーリエ変換は連続・非周期のまま,離散フーリエ変換は離散的・周期的のまま,時間領域と周波数領域を行ったり来たりする変換だ.それに対して,フーリエ級数展開と離散時間フーリエ変換は,「連続・周期的」と「離散的・非周期的」が入れ替わりながら行ったり来たりする変換になる.
あと,さっき出てきた「高速フーリエ変換」は,あくまで「離散フーリエ変換」の高速計算方法だってことには注意しておこう.
swk(at)ic.is.tohoku.ac.jp