: 6. 離散フーリエ変換 : やる夫で学ぶディジタル信号処理 : 4. 離散時間信号 目次 アイコンを表示する
![$\displaystyle = \left\{\begin{array}{ll} f[n], & t = n 0, & \text{otherwise} \end{array}\right.$](img416.png) |
(5.1) |
![\includegraphics[scale=0.5]{fig_dtft/fn_ft.eps}](img417.png)
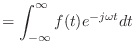 |
(5.2) |
![\includegraphics[scale=0.5]{fig_dtft/fn_e-jwn.eps}](img426.png)
![\includegraphics[scale=0.5]{fig_dtft/ft_delta.eps}](img428.png)
式で書くならこうなる.
![$\displaystyle = \sum_{n = -\infty}^{\infty} f[n]\delta(t - n)$](img429.png) |
(5.4) |
![$\displaystyle = \int_{-\infty}^{\infty} \left\{ \sum_{n = -\infty}^{\infty} f[n]\delta(t - n) \right\} e^{-j\omega t} dt$](img430.png) |
(5.5) | |
![$\displaystyle = \sum_{n = -\infty}^{\infty} f[n] \int_{-\infty}^{\infty} \delta(t - n) e^{-j\omega t} dt$](img431.png) |
(5.6) | |
![$\displaystyle = \sum_{n = -\infty}^{\infty} f[n] e^{-j\omega n}$](img427.png) |
(5.7) |
![\includegraphics[scale=0.5]{fig_dtft/periodic_ft.eps}](img433.png)
![\includegraphics[scale=0.5]{fig_dtft/discrete_ft.eps}](img436.png)
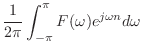 |
(5.9) | |
![$\displaystyle \frac{1}{2\pi}\int_{-\pi}^{\pi} \left\{ \sum_{m = -\infty}^{\infty} f[m] e^{-j\omega m} \right\} e^{j\omega n} d\omega$](img444.png) |
(5.10) |
![$\displaystyle \frac{1}{2\pi} \sum_{m = -\infty}^{\infty} f[m] \int_{-\pi}^{\pi} e^{j\omega (n - m)} d\omega$](img445.png) |
(5.11) | |
![$\displaystyle \frac{1}{2\pi} \sum_{m = -\infty}^{\infty} f[m] \cdot 2\pi \delta_{m,n}$](img446.png) |
(5.12) | |
| (5.13) |
まとめよう.
| (5.14) | ||
| (5.15) | ||
| (5.16) | ||
| (5.17) | ||
| (5.18) |
周波数領域では,我々は ![]() みたいに大文字の変数を使う場合は非正規化周波数,
みたいに大文字の変数を使う場合は非正規化周波数,![]() のような小文字の場合は正規化周波数ということにしているので,まあそれである程度判断できるかな.もっとはっきり区別したいときに,離散時間フーリエ変換
のような小文字の場合は正規化周波数ということにしているので,まあそれである程度判断できるかな.もっとはっきり区別したいときに,離散時間フーリエ変換 ![]() を
を
swk(at)ic.is.tohoku.ac.jp