: 11. スペクトル解析と窓関数 : やる夫で学ぶディジタル信号処理 : 9. フーリエ変換の性質(3): パーセバルの等式 ― 目次 アイコンを表示する
![\includegraphics[scale=0.5]{fig_sampling/interpolation.eps}](img767.png)
だが実は,元の信号に割と現実的な制約条件を考えてやることで,その常識的な想像を覆すことができる.つまり,サンプリングされた信号から,元の連続時間信号を完全に復元することができる.シャノンのサンプリング定理,あるいは標本化定理と呼ばれる有名な結果だ.
| (10.1) |
このとき,サンプリング周波数
![]() が
が
| (10.2) |
つまり,元の信号の帯域の 2 倍を超える周波数でサンプリングしておけば,完全復元が可能ということだ.
元の連続時間信号を ![]() としよう.周波数領域で見ると
としよう.周波数領域で見ると ![]() だ.
だ.
| (10.3) |
![\includegraphics[scale=0.5]{fig_sampling/orig_sig.eps}](img778.png)
これをサンプリング周波数
![]() ,つまりサンプリング周期
,つまりサンプリング周期
![]() でサンプリングして離散時間信号
でサンプリングして離散時間信号
![]() を得たとしよう.
を得たとしよう.
| (10.4) |
![\includegraphics[scale=0.5]{fig_sampling/sampling_xt.eps}](img781.png)
| (10.5) | ||
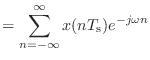 |
(10.6) |
これからやるのは,端的に言うと,この
![]() から
から ![]() を完全に復元できるかという問題を考えようということだ.
を完全に復元できるかという問題を考えようということだ.
![\includegraphics[scale=0.5]{fig_sampling/xd_omega.eps}](img788.png)
| (4.3) |
![\includegraphics[scale=0.5]{fig_sampling/xd_omega_nonnorm.eps}](img796.png)
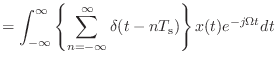 |
(10.8) |
![$\displaystyle = {\cal F}\left[\left\{\sum_{n = -\infty}^{\infty}\delta(t - nT_\textnormal{s})\right\} x(t)\right]$](img799.png) |
(10.9) |
![\includegraphics[scale=0.5]{fig_sampling/xd_omega_comb.eps}](img802.png)
ここで右辺にたたみこみと積の関係 (式(8.29)) を使うと,
![$\displaystyle = \frac{1}{2\pi}{\cal F}\left[\sum_{n = -\infty}^{\infty}\delta(t - nT_\textnormal{s})\right] * X(\Omega)$](img803.png) |
(10.10) |
ここまでの話をざっくりまとめると,サンプリングするということは,すなわち
![]() をかけることに相当している.これを周波数領域で見ると,
をかけることに相当している.これを周波数領域で見ると,
![]() のフーリエ変換をたたみこむことを意味する.
のフーリエ変換をたたみこむことを意味する.
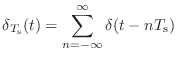 |
(10.11) |
![\includegraphics[scale=0.5]{fig_sampling/fourier_comb_question.eps}](img810.png)
ちゃんと計算で示しておこうと思う.ただし,ちょっと技巧的になるけどな.まず,くし型関数
![]() が周期
が周期
![]() の周期関数であることに注意して,フーリエ級数展開しておく.
の周期関数であることに注意して,フーリエ級数展開しておく.
![$\displaystyle = \sum_{k = -\infty}^{\infty} \left[ \frac{1}{T_\textnormal{s}} \...
...\delta(t) e^{-j\Omega_\textnormal{s}kt} dt \right] e^{j\Omega_\textnormal{s}kt}$](img812.png) |
(10.13) | |
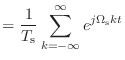 |
(10.14) |
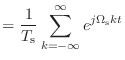 |
(10.15) | |
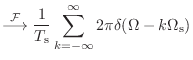 |
(10.16) | |
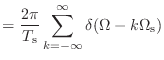 |
(10.17) | |
| (10.18) |
| (10.19) |
![\includegraphics[scale=0.5]{fig_sampling/fourier_comb.eps}](img820.png)
| (10.12) |
| (10.20) | ||
| (10.21) |
![$\displaystyle = \frac{1}{T_\textnormal{s}}\left[\sum_{k = -\infty}^{\infty} \delta(\Omega - k\Omega_\textnormal{s})\right] * X(\Omega)$](img824.png) |
(10.22) | |
![$\displaystyle = \frac{1}{T_\textnormal{s}} \int_{-\infty}^{\infty} \left[\sum_{k = -\infty}^{\infty} \delta(W - k\Omega_\textnormal{s})\right] X(\Omega - W)dW$](img825.png) |
(10.23) | |
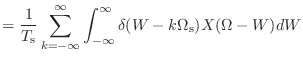 |
(10.24) | |
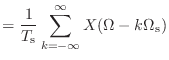 |
(10.25) |
| (10.26) |
![\includegraphics[scale=0.5]{fig_sampling/response_shift.eps}](img830.png)
じゃあ,入力として
![]() を入れた場合はどうなる?
を入れた場合はどうなる?
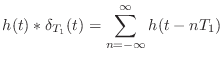 |
(10.27) |
![\includegraphics[scale=0.5]{fig_sampling/response_comb.eps}](img835.png)
| (10.21) | ||
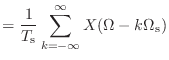 |
(10.28) |
![\includegraphics[scale=0.5]{fig_sampling/convolved_x_omega.eps}](img836.png)
このときのサンプリング後のスペクトル
![]() はどんな形になる?
はどんな形になる?
![\includegraphics[scale=0.5]{fig_sampling/convolved_x_omega_bandlimit.eps}](img839.png)
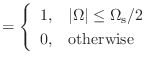 |
(10.30) |
![\includegraphics[scale=0.5]{fig_sampling/reconst_in_freq.eps}](img844.png)
ちょっと面倒ではあるんだが,ゆっくり考えてみようか.式(10.29) を時間領域で考えると
| (10.31) | ||
![$\displaystyle = h_\textnormal{r}(t) * \left( \sum_n x_\textnormal{d}[n] \delta(t - nT_\textnormal{s}) \right)$](img848.png) |
(10.32) |
![\includegraphics[scale=0.5]{fig_sampling/relation_dtft_ft.eps}](img850.png)
つまり
![]() を
を
![]() だけシフトして
だけシフトして
![]() 倍したものを全
倍したものを全 ![]() について足し合わせたのが
について足し合わせたのが ![]() だ.これもある種のたたみこみととらえればいいんだが,離散信号
だ.これもある種のたたみこみととらえればいいんだが,離散信号
![]() と連続信号
と連続信号
![]() の離散たたみこみになっているのがややこしいところだ.
の離散たたみこみになっているのがややこしいところだ.
| (10.33) | ||
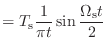 |
(10.34) | |
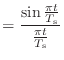 |
(10.35) |
![\includegraphics[scale=0.5]{fig_sampling/norm_sincs.eps}](img859.png)
![\includegraphics[scale=0.5]{fig_sampling/reconst_in_time.eps}](img860.png)
![\includegraphics[scale=0.5]{fig_sampling/xd_omega_undersampled.eps}](img862.png)
![\includegraphics[scale=0.5]{fig_sampling/xd_omega_undersampled_150hz.eps}](img864.png)
折り返しってのは今の 75 Hz で折り返す意味の折り返しかお.
レートも周波数も本質的には同じ概念を指す言葉だが,レートの方が使える文脈が限られているんだな.つまり「単位時間あたり何回サンプルできるか」という意味のサンプリング周波数の代わりに「サンプリングレート」という言葉を使うことはできるが,「信号が 100 Hz の周波数成分を含む」という代わりに「100 Hz のレート成分を含む」とはちょっと言い難い.ということを考えると,「ナイキストレート」という言葉は「サンプリングレートの下限」の方にしか使えなさそうってのはまあ納得のいくところだ.
 |
(10.36) |
| (10.37) |
だから
![]() にしろ
にしろ
![]() にしろ,
にしろ,
![]() のところでのみ値を持ってほかは 0,という表現を共通して選んでいるわけだ.サンプリングという操作の表現としてはまあ自然なものだろう.
のところでのみ値を持ってほかは 0,という表現を共通して選んでいるわけだ.サンプリングという操作の表現としてはまあ自然なものだろう.
![\includegraphics[scale=0.5]{fig_sampling/sampling_xt_by_comb.eps}](img871.png)
これを周波数領域で見るとどうなる?
![\includegraphics[scale=0.5]{fig_sampling/dtft_by_comb.eps}](img872.png)
![\includegraphics[scale=0.5]{fig_sampling/fs_by_comb.eps}](img873.png)
あるいは,フーリエ級数展開からスタートしてもいい.
swk(at)ic.is.tohoku.ac.jp