- やらない夫
- ところで離散時間信号では,連続時間のときの常識が通用しない場合があるんだ.そういう例について話しておこうと思う.
- やる夫
- なんだお,どきどきするお.
- やらない夫
- さっき,
![$\displaystyle x[n]$](img387.png) |
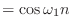 |
(4.5) |
の周期を
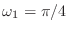 の場合について考えただろう.同じことを
の場合について考えただろう.同じことを
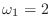 について考えるとどうなる?
について考えるとどうなる?
- やる夫
- なんだ,そんなの同じく考えればいいんだお?
角周波数が
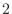 なんだから,周期は
なんだから,周期は
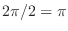 になるお.
になるお.
- やらない夫
- 本当にそう思うか?
- やる夫
- …? そりゃ思うお.
- やらない夫
- グラフをかいてみてくれ.
- やる夫
- 簡単だお.時刻が 1 進むごとに 2 [rad] 位相が進むんだお.それで,時刻が
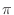 進んだときにちょうど cos が 1 周…,あれ?
進んだときにちょうど cos が 1 周…,あれ? 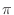 は整数じゃないから,ちょうど cos が 1 周するようなところに信号の値は無いんだお.これってどうなるのかお….
は整数じゃないから,ちょうど cos が 1 周するようなところに信号の値は無いんだお.これってどうなるのかお….
- やらない夫
- そこが核心だ.つまり,
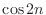 は周期信号じゃないんだ.三角関数とか,あとは複素指数関数もそうだが,離散時間の場合は常に周期的とは限らない.連続時間で考えたときにちょうど 1 周するような時刻がたまたま整数になっているときだけ,離散時間でも周期的になる.この辺が離散時間信号の第一の落とし穴だ.
は周期信号じゃないんだ.三角関数とか,あとは複素指数関数もそうだが,離散時間の場合は常に周期的とは限らない.連続時間で考えたときにちょうど 1 周するような時刻がたまたま整数になっているときだけ,離散時間でも周期的になる.この辺が離散時間信号の第一の落とし穴だ.
- やる夫
- うー,意地悪だお.三角関数が周期的じゃないなんて,気持ち悪いお.…って「第一」のって何だお.まだあるのかお.
- やらない夫
- ああ.そしてこっちの方がもっと気持ち悪いかも知れない.結論を一言でいうと,離散時間の三角関数や複素指数関数は,角周波数を
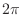 増やすと元の関数に戻る.
増やすと元の関数に戻る.
- やる夫
- 元に戻る? 何言ってるかさっぱりわからんお.
- やらない夫
- つまり,こういうことだ.また角周波数
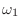 の cos 関数を考えよう.
の cos 関数を考えよう.
![$\displaystyle x[n]$](img387.png) |
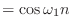 |
(4.6) |
- やる夫
- さっきと同じだお.
- やらない夫
- この関数で,角周波数が
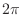 だけ大きくなったらどうなる?
だけ大きくなったらどうなる?
- やる夫
- どうなるって,周波数が大きくなるんだから,振動が速くなるお.式で書くなら
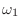 のところに
のところに
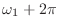 を代入するだけだお.
を代入するだけだお.
| |
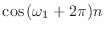 |
(4.7) |
これがどうかしたかお?
- やらない夫
- もう少し変形してみようか.
| |
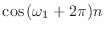 |
(4.8) |
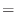 |
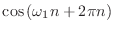 |
(4.9) |
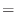 |
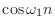 |
(4.10) |
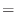 |
![$\displaystyle x[n]$](img387.png) |
(4.11) |
これが任意の整数 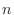 について成り立つ.cos の位相が
について成り立つ.cos の位相が 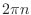 増えるってことは
増えるってことは 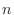 周して元に戻るってことだからな.
周して元に戻るってことだからな.
- やる夫
![$ x[n]$](img404.png) の角周波数を
の角周波数を 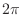 増やしたらまた
増やしたらまた ![$ x[n]$](img404.png) になったってことだお.…えっ? これどういうことだお?
になったってことだお.…えっ? これどういうことだお?
- やらない夫
- 今の話は
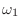 の値によらず成り立つ.sin でも,複素指数関数でも同じだ.つまり,何か適当な三角関数や複素指数関数があったとして,その角周波数を
の値によらず成り立つ.sin でも,複素指数関数でも同じだ.つまり,何か適当な三角関数や複素指数関数があったとして,その角周波数を 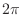 大きくしたら,元の関数に戻るってことだ.
大きくしたら,元の関数に戻るってことだ.
- ポルナレフ
- あ…ありのまま 今 起こった事を話すぜ!
『おれは 角周波数を上げていたと思ったら いつのまにか元の関数に戻っていた』
な… 何を言ってるのか わからねーと思うが おれも 何をされたのかわからなかった…
- やる夫
- いや,あんた誰だお.
- やらない夫
- まあ,実際あり得ないことだろ,連続時間の常識的に考えて….ところが,離散時間の世界ではむしろこれが常識なんだ.
- やる夫
- よくわからんお.どうしてそんなことが起きるんだお.
- やらない夫
- 「角周波数を
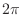 増やす」というのは,どういう意味になる?
増やす」というのは,どういう意味になる?
- やる夫
- ええと,正規化角周波数なんだから,1 サンプル時間あたりに進む位相が
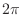 増えるってことだお.つまり,1 サンプル時間あたりに振動する回数が
1 回増えるってことだお.
増えるってことだお.つまり,1 サンプル時間あたりに振動する回数が
1 回増えるってことだお.
- やらない夫
- そうだな.グラフで考えようか.これが
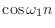 だ.1 時刻で
だ.1 時刻で
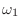 だけ位相が進んでいる.点線が連続時間のコサイン関数で,サンプリングしたものを実線の縦棒で描いている.
だけ位相が進んでいる.点線が連続時間のコサイン関数で,サンプリングしたものを実線の縦棒で描いている.
- やる夫
- そうなるお.
- やらない夫
- 角速度が
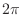 増えるってのは,1 時刻に「もう 1 周分だけ」余計に回るってことだ.それを一点鎖線で示そう.
増えるってのは,1 時刻に「もう 1 周分だけ」余計に回るってことだ.それを一点鎖線で示そう.
- やる夫
- あー,各サンプル時刻だけ見たら全く同じだお!
余計に回るのはちょうど1 周だけから,1 時刻後の位相は同じになるんだお.
- やらない夫
- そういうことだ.あくまで時刻が整数のところの値しか考えないってことに注意しなくちゃならない.三角関数とか複素指数関数を見ると,つい時刻間の点線の部分を頭の中で想像してしまいがちだが,実際には点線の部分は「存在しない」んだ.だから,角周波数が
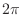 増えるごとに元の信号に戻ってしまう.
増えるごとに元の信号に戻ってしまう.
- やる夫
- うーん,一応納得はしたけど,やっぱり不思議だお.
- やらない夫
- 慣れるしかないかな.具体的な信号を見てみるとわかりやすいかも知れない.例えば,
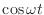 を角周波数変えながらプロットしてみるとこんな風になる.上から順に
を角周波数変えながらプロットしてみるとこんな風になる.上から順に 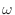 が 0 から
が 0 から 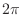 まで増えていっている.横軸は時間で,点線は,連続時間信号だった場合のプロットだ.同じものが離散時間信号だと縦棒で示した点になる.
まで増えていっている.横軸は時間で,点線は,連続時間信号だった場合のプロットだ.同じものが離散時間信号だと縦棒で示した点になる.
- やる夫
- 大軍だお.
- やらない夫
- 連続時間だと角周波数が増えるにしたがってどんどん振動が速くなっていく.これはわかるな? ところがこれをサンプリングすると,
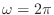 で
で
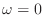 と同じになる.つまり直流に戻るんだな.
と同じになる.つまり直流に戻るんだな.
で,同じように 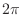 から
から 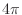 まで角周波数を増やしていくとこうなる.
まで角周波数を増やしていくとこうなる.
- やる夫
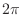 を過ぎて,そのまま角周波数を増やしていっても,0 〜
を過ぎて,そのまま角周波数を増やしていっても,0 〜 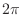 の間の繰り返しになってるわけだお.
の間の繰り返しになってるわけだお.
- やらない夫
- そういうことだ.もう一つ気づいて欲しいのは,離散時間信号だと
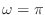 のときが一番振動が速いってことだ.そこから
のときが一番振動が速いってことだ.そこから 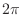 にかけてどんどん遅くなっていって直流に戻る.
にかけてどんどん遅くなっていって直流に戻る.
- やる夫
- あー,つい点線を見てしまうけど,縦棒だけを見ると,
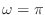 を境に対称に直流まで戻っていくお.
を境に対称に直流まで戻っていくお.
- やらない夫
- なので,繰り返しの区間が 0 〜
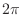 だと思わずに,
だと思わずに,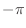 〜
〜 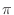 だと考える方がわかりやすいだろうな.実際,ディジタル信号処理ではそのように考えることが多いんだ.
だと考える方がわかりやすいだろうな.実際,ディジタル信号処理ではそのように考えることが多いんだ.
角周波数 0,つまり直流を中心として,そこからちょっと角周波数が増えると小さな正の周波数になって,ちょっと減ると小さな負の周波数になる.正とか負の周波数っていう概念は以前話した通りだな.そして最も高周波なのが,角周波数が 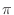 あるいは
あるいは 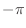 のときだ.この範囲外に角周波数を上げようとしても,結局
のときだ.この範囲外に角周波数を上げようとしても,結局 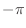 〜
〜 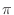 の範囲を繰り返すだけになる.
の範囲を繰り返すだけになる.
- やる夫
- そう言えば,周波数成分を考えるときは,正の周波数と負の周波数を組にして考えるとわかりやすかったんだお.そういう点でも,
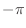 〜
〜 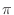 の範囲で考える方が便利そうだお.
の範囲で考える方が便利そうだお.
- やらない夫
- というわけで,三角関数にしろ複素指数関数にしろ,角周波数ってのは,
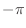 〜
〜 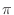 の範囲だけを考えれば十分だってことだ.この話は今後かなり重要になってくるので,よく理解しておいて欲しい.
の範囲だけを考えれば十分だってことだ.この話は今後かなり重要になってくるので,よく理解しておいて欲しい.
![\includegraphics[scale=0.5]{fig_dtsig/sampling_ft_fn.eps}](img384.png)
![\includegraphics[scale=0.5]{fig_dtsig/sampling_cos.eps}](img391.png)
![\includegraphics[scale=0.5]{fig_dtsig/sampling_cos_n2.eps}](img397.png)
![\includegraphics[scale=0.5]{fig_dtsig/sampling_cos_w1.eps}](img406.png)
![\includegraphics[scale=0.5]{fig_dtsig/sampling_cos_w1_2pi.eps}](img407.png)
![\includegraphics[scale=1.0]{cos_0_2pi.eps}](img409.png)
![]() から
から ![]() まで角周波数を増やしていくとこうなる.
まで角周波数を増やしていくとこうなる.
![\includegraphics[scale=1.0]{cos_2pi_4pi.eps}](img413.png)
![]() あるいは
あるいは ![]() のときだ.この範囲外に角周波数を上げようとしても,結局
のときだ.この範囲外に角周波数を上げようとしても,結局 ![]() 〜
〜 ![]() の範囲を繰り返すだけになる.
の範囲を繰り返すだけになる.