- やらない夫
- さて,実際にそういう極限を考えたときに,数式としてはどんな形になるのかっていうのが次の話だ.ところがちょっと問題があって,今の話の流れで考えていても,実は答えにはたどり着けないんだ.
- やる夫
- ちゃぶ台返しかお.じゃあ今までの話はなんだったんだお.
- やらない夫
- まあそう言うな.飛び飛びの離散周波数から連続周波数になっていくイメージを持ってもらいたかっただけだ.でも,どんなに間隔が細かくなっても線は線のままだからな.そのままじゃ連続にはならない.なのでそこはちょっと連続化のための手続きを踏んでやる必要がある.
- やる夫
- どういうことかお.
- やらない夫
- フーリエ級数展開の式から出発しよう.前回の式(2.18),つまりこれだ.
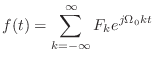 |
(3.1) |
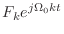 を整数
を整数 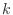 について総和しているわけだ.これはいいな?
について総和しているわけだ.これはいいな?
- やる夫
- OKだお.
- やらない夫
- スペクトルの間隔
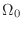 をどんなに細かくしていっても,総和のままじゃダメなんだ.周波数が連続化されて,総和が積分になるように話を持っていきたい.
をどんなに細かくしていっても,総和のままじゃダメなんだ.周波数が連続化されて,総和が積分になるように話を持っていきたい.
- やる夫
- よく話が見えないお.
- やらない夫
- 具体的に見ていこうか.このグラフが
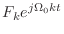 を表していると思ってくれ.
を表していると思ってくれ.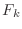 じゃなくて,
じゃなくて,
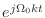 をかけた後,でも総和を取る前のグラフだ.
をかけた後,でも総和を取る前のグラフだ.
この線の長さを全部足すと 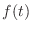 になる,ってのがフーリエ級数の意味するところだ.長さっていっても本当は複素数だという点には注意しなきゃいけないんだが,ともかくこうやって表そう.
になる,ってのがフーリエ級数の意味するところだ.長さっていっても本当は複素数だという点には注意しなきゃいけないんだが,ともかくこうやって表そう.
- やる夫
- わかるお.フーリエ級数の式そのものだお.
- やらない夫
- ところが,このまま線の間隔を狭くしていっても,線のままだといつまでたっても連続にならないってのが問題だったわけだ.だから,こんな風に線の長さじゃなくて面積になるように書き換えよう.
- やる夫
- えっと,これはどういうことだお.
- やらない夫
- 線の代わりに横幅
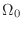 の短冊みたいなのを考える.この短冊の面積が,元の線の長さ,つまり
の短冊みたいなのを考える.この短冊の面積が,元の線の長さ,つまり
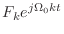 と等しくなるようにする.すると短冊の高さはどうなる?
と等しくなるようにする.すると短冊の高さはどうなる?
- やる夫
- んー,
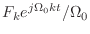 でいいのかお?
でいいのかお? 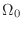 で割っただけだお.
で割っただけだお.
- やらない夫
- そういうことだ.これで,この短冊の面積をすべて足し合わせると
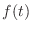 になるようにできたわけだ.こうやって「総和を計算する問題」を「面積を計算する問題」に書き換えておいてから,分割をどんどん細かくしていけば,「面積を積分で求める問題」に持って行くことができる.
になるようにできたわけだ.こうやって「総和を計算する問題」を「面積を計算する問題」に書き換えておいてから,分割をどんどん細かくしていけば,「面積を積分で求める問題」に持って行くことができる.
- やる夫
- うーん,なんか微妙にしっくり来ないけど,そんなもんなのかお.
- やらない夫
- 同じ無限でも,「整数が無限にある」というときの無限と「実数が無限にある」というときの無限との間には大きなギャップがあるんだ.だから「線」のまま間隔を狭くしていっても連続にはならない.そのギャップを,面積を持つ短冊を考えることで埋めていると思ってくれ.
今の話を数式で書くとこうなる.まずフーリエ級数の式を,面積の総和だと思って書き換える.
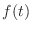 |
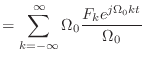 |
(3.2) |
- やる夫
- 横×縦の総和に書き換えたわけだお.
- やらない夫
- で,理由は後で説明するが,何も聞かずにここで
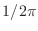 をくくり出してくれ.
をくくり出してくれ.
- やる夫
- ええー,まあ聞くなというなら聞かないけど,気持ち悪いお.
- やらない夫
- うん,あとで説明するから勘弁してほしい.で,ここで新しい変数をいくつか導入しておこう.まず
![$ \Omega[k] = \Omega_0 k$](img218.png) とする.基本角周波数の
とする.基本角周波数の 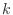 倍の値を持つ角周波数だ.丸括弧じゃなくて角括弧なのは,括弧の中身が整数だということを強調しているつもりだ.
倍の値を持つ角周波数だ.丸括弧じゃなくて角括弧なのは,括弧の中身が整数だということを強調しているつもりだ.
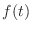 |
![$\displaystyle = \frac{1}{2\pi}\sum_{k=-\infty}^{\infty} \Omega_0 \frac{2\pi F_k e^{j\Omega[k] t}}{\Omega_0}$](img219.png) |
(3.4) |
- やる夫
- 整数
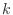 によって変わる角周波数を表す変数だと考えるわけだお.
によって変わる角周波数を表す変数だと考えるわけだお.
- やらない夫
- そして,総和の中の項のうち
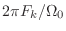 の部分を
の部分を
![$ F(\Omega[k])$](img221.png) と書くことにする.
と書くことにする.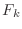 の定数倍だから,周波数スペクトルを表す量になる.
の定数倍だから,周波数スペクトルを表す量になる.
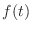 |
![$\displaystyle = \frac{1}{2\pi}\sum_{k=-\infty}^{\infty} \Omega_0 F(\Omega[k]) e^{j\Omega[k] t}$](img222.png) |
(3.5) |
- やる夫
- ん,なんで
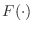 の中に
の中に ![$ \Omega[k]$](img224.png) が出てくるのかお?
が出てくるのかお? ![$ F[k]$](img225.png) じゃだめなのかお.
じゃだめなのかお.
- やらない夫
- そうだな,今の時点では
![$ F[k]$](img225.png) だと考える方が自然かもしれない.
だと考える方が自然かもしれない.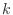 という整数に応じて値が決まるわけだからな.でも,後から積分に移行するときに備えてここは角周波数の単位を持つ量で書いておきたいんだ.つまり,
という整数に応じて値が決まるわけだからな.でも,後から積分に移行するときに備えてここは角周波数の単位を持つ量で書いておきたいんだ.つまり,
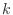 という整数に応じて
という整数に応じて ![$ \Omega[k]$](img224.png) という角周波数が決まって,その角周波数のスペクトル成分
という角周波数が決まって,その角周波数のスペクトル成分
![$ F(\Omega[k])$](img221.png) が与えられると考えておく.
が与えられると考えておく.
- やる夫
- 何かさっきから後の都合ばっかりだお.
- やらない夫
-
![$ F(\Omega[k])$](img221.png) の計算式も書き下しておこう.
の計算式も書き下しておこう.
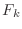 を計算する式 (2.28) で,
を計算する式 (2.28) で,
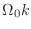 を
を ![$ \Omega[k]$](img224.png) と書いてやると,こうなる.
と書いてやると,こうなる.
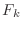 |
![$\displaystyle = \frac{1}{T_0} \int_{-T_0/2}^{T_0/2} f(t) e^{-j\Omega[k]t}dt$](img227.png) |
(3.6) |
これを
![$ F(\Omega[k]) = 2\pi F_k / \Omega_0$](img228.png) に代入して
に代入して
になる.
- やる夫
- ええと,
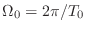 だから確かにそうなるお.
だから確かにそうなるお.
![$ F(\Omega[k])$](img221.png) が
が ![$ \Omega[k]$](img224.png) によって決まる量になっているのもわかるお.
によって決まる量になっているのもわかるお.
- やらない夫
- それから,
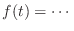 の式に戻って,これは単に変数名の置き換えだと思ってもらえばいいんだが,
の式に戻って,これは単に変数名の置き換えだと思ってもらえばいいんだが,
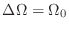 とする.
とする.
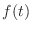 |
![$\displaystyle = \frac{1}{2\pi}\sum_{k=-\infty}^{\infty} F(\Omega[k]) e^{j\Omega[k] t} \Delta\Omega$](img234.png) |
(3.9) |
- やる夫
- んー,どうして
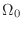 のままじゃダメなのかお?
のままじゃダメなのかお?
- やらない夫
- 別にダメじゃないんだが,単に,積分に移行するときにわかりやすくするためだと思ってくれ.書く場所を右辺の一番後ろに移したのもそのためだ.
- やる夫
- ふーん,まあいいお.
- やらない夫
- さて,ここまでで準備完了だ.
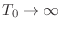 の極限を考えてやる.
の極限を考えてやる.
![$ \Omega[k]$](img224.png) は実数
は実数 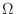 に連続化されて,
に連続化されて,
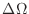 は無限小になって
は無限小になって 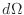 になる.
になる.
で,途中で計算しておいた式 (3.8) の
![$ F(\Omega[k])$](img221.png) の方も,同様に
の方も,同様に
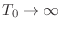 の極限を考える.単純に積分の範囲が無限大に飛んでいくだけだな.これをフーリエ変換と呼ぶ.
の極限を考える.単純に積分の範囲が無限大に飛んでいくだけだな.これをフーリエ変換と呼ぶ.
そしてさっきの式 (3.10) の方をフーリエ逆変換と呼ぶ.
- やる夫
- いつの間にか「級数展開」が「変換」になったお.
- やらない夫
- いつの間にかというか,いつ「変換」になったかと敢えて答えるなら,無限に飛ばして連続化したときだな.その時点で「連続時間上の関数」と「連続周波数上の関数」の相互間の「変換」になったと考えている.
フーリエ変換の計算式の右辺には時間変数 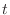 と周波数変数
と周波数変数 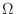 が含まれているが,
が含まれているが,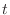 で積分するから,
で積分するから,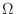 だけが残る.連続時間上の関数から連続周波数上の関数への変換になるわけだ.フーリエ逆変換の方は,右辺を
だけが残る.連続時間上の関数から連続周波数上の関数への変換になるわけだ.フーリエ逆変換の方は,右辺を 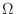 で積分しているから,
で積分しているから,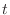 だけが残るんだな.時間関数への変換になる.
だけが残るんだな.時間関数への変換になる.
- やる夫
- 結局,周波数が連続になっただけで,フーリエ級数と同じようなものだと思っていいのかお?
- やらない夫
- そうだな,基本的な考え方は同じだ.フーリエ級数は,周期的な時間信号を無限個の複素指数関数の足し合わせで表現したわけだ.ただし無限といっても高々「整数の個数」の無限だ.周波数成分は飛び飛びにしか存在しないが,それで元の時間関数が十分に再現できた.
これに対して,周期的とは限らない一般の時間信号を表現しようと思うと.周波数としてはあらゆる実数を考えなくてはならなくなる.数式で表現すると複素指数関数の「総和」ではなくて「積分」で表現しなくてはならないわけだ.
- やる夫
- フーリエ級数の「複素指数関数の足し合わせで表す」っていう考え方は直観的にわかりやすかったお.でも総和じゃなくて積分になるとどうもピンと来ないお.
- やらない夫
- そうかもしれないが,本質的には全く同じことなんだ.同じイメージを持っていて構わない.ただし「足し合わせ」という言葉を使うのはさすがに違和感があるので,「重ね合わせ」という言葉を使うことが多い.
- やる夫
- 「重ね合わせの原理」とかいう場合の重ね合わせと同じかお?
- やらない夫
- そうだな.「重ね合わせ」という言葉であれば,総和の場合も積分の場合も,まあそんなに違和感無く表現できてる気がするが,どうだろう.まあ語感は人それぞれかも知れないけどな.
ともかく,一般の時間信号は,あらゆる実数を周波数とする複素指数関数の重ね合わせで表すことができる,ということだ.これがフーリエ逆変換の意味だ.
- やる夫
- 逆? あ,そうか,フーリエ級数展開に対応するのは,フーリエ変換じゃなくてフーリエ逆変換の方なんだお.なんか混乱しそうだお.
- やらない夫
- そう,フーリエ変換は,フーリエ係数の計算の方に対応している.それぞれの周波数成分がどのくらい含まれているかを知るための計算になっているということだな.
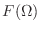 は一般に複素数になるから,振幅と位相を持っている.フーリエ係数
は一般に複素数になるから,振幅と位相を持っている.フーリエ係数 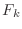 と同様に,周波数
と同様に,周波数 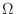 の成分の振幅と初期位相を表しているわけだ.
の成分の振幅と初期位相を表しているわけだ.
- やる夫
- フーリエ級数展開やフーリエ係数の計算を「変換」と呼んじゃダメなのかお?
- やらない夫
- ダメってことはないし,変換だと理解して構わないと思うぞ.単に歴史的な事情で「級数展開」だと解釈されるのが普通だというだけだ.級数展開だろうが変換だろうが,信号を複数の周波数に分解しているんだという点には変わりがない.周波数が飛び飛びか,連続かという違いはあるけどな.
- やる夫
- こうして見比べると,フーリエ変換とフーリエ逆変換の式ってほとんど似たようなもんだお.指数部にマイナスがついているかどうかと,定数倍があるかないかだけの違いだお.
- やらない夫
- そうだな.まあ,どっちを変換と呼んでどっちを逆変換と呼ぶかなんてのは,単に慣例的なものだ.時間 → 周波数の方向を変換,反対方向を逆変換と呼ぶと約束したに過ぎない.
ついでに言うと,さっきの式 (3.3) のところで 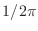 をくくり出したのも,同じように単に慣例的なものなんだ.
をくくり出したのも,同じように単に慣例的なものなんだ.
- やる夫
- ああ,後から説明するって言われてたのを忘れてたお.結局どういうことなんだお?
- やらない夫
- あそこで
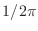 をくくり出さなかったどうなるか,計算してみればわかるんだが,フーリエ変換の式の方の先頭に
をくくり出さなかったどうなるか,計算してみればわかるんだが,フーリエ変換の式の方の先頭に 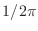 がついて,逆変換の式の方には何もつかなくなるんだ.だから,「フーリエ変換」の式をきれいに見せたかったら今回みたいに
がついて,逆変換の式の方には何もつかなくなるんだ.だから,「フーリエ変換」の式をきれいに見せたかったら今回みたいに 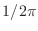 でくくればいいし,「フーリエ逆変換」の式をきれいに見せたいならば,くくらずに導出したもので定義すればよかった.どっちにしろ,フーリエ変換して,またフーリエ逆変換すればちゃんと元に戻るからな.どっちでもよいんだけど,我々は前者を採用したってことだ.教科書によっては両方に
でくくればいいし,「フーリエ逆変換」の式をきれいに見せたいならば,くくらずに導出したもので定義すればよかった.どっちにしろ,フーリエ変換して,またフーリエ逆変換すればちゃんと元に戻るからな.どっちでもよいんだけど,我々は前者を採用したってことだ.教科書によっては両方に
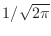 をつけているのもあるしな.
をつけているのもあるしな.
- やる夫
- どっちでもいいってのはあまり納得いかないお.定義が変わったら周波数成分の値が定数倍だけ変わってしまうお.
- やらない夫
- 変わってもいいんだよ.例えばもとの時間信号の振幅が,そうだな,電圧だったとしようか.じゃあそれをフーリエ変換したときの周波数成分の単位はどうなる?
- やる夫
- えっ? えーと,電圧を時間積分してるんだから,電圧×時間の次元になるのかお.あまり普段使うような単位じゃなさそうだお.
- やらない夫
- だな.だから,その値が
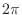 倍になってようがいまいが,その絶対的な数値自体は大した問題じゃない.長さをヤードで測るかメートルで測るか尺で測るかによって数値が変わるのと同じだ.ただし,どの定義で計算したものかはちゃんと把握しておかないとわけがわからなくなるので注意した方がいい.いろんな教科書の公式を混ぜて使うのは危険だ.
倍になってようがいまいが,その絶対的な数値自体は大した問題じゃない.長さをヤードで測るかメートルで測るか尺で測るかによって数値が変わるのと同じだ.ただし,どの定義で計算したものかはちゃんと把握しておかないとわけがわからなくなるので注意した方がいい.いろんな教科書の公式を混ぜて使うのは危険だ.
というわけでまとめよう.ついでにいくつか記号や用語も導入しておこう.
- 連続時間
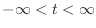 で定義された関数
で定義された関数 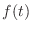 (のうち実用上重要なものの多く) に対して,式 (3.11) で計算される
(のうち実用上重要なものの多く) に対して,式 (3.11) で計算される 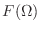 を
を 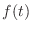 のフーリエ変換と呼ぶ.(あるいはこの計算をすること自体をフーリエ変換と呼ぶ)
のフーリエ変換と呼ぶ.(あるいはこの計算をすること自体をフーリエ変換と呼ぶ)
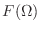 から,式 (3.10) によって元の
から,式 (3.10) によって元の 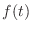 が復元できる.この計算をフーリエ逆変換と呼ぶ.(あるいは「
が復元できる.この計算をフーリエ逆変換と呼ぶ.(あるいは「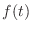 は
は
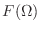 のフーリエ逆変換である」という言い方もする)
のフーリエ逆変換である」という言い方もする)
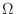 は角周波数を表す連続変数である.
は角周波数を表す連続変数である.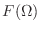 は
は 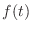 に含まれる角周波数
に含まれる角周波数 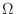 の振動成分の量 (振幅・位相) を表す.
の振動成分の量 (振幅・位相) を表す.
-
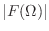 ,
,
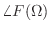 ,
,
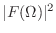 をそれぞれ,
をそれぞれ,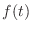 の振幅スペクトル,位相スペクトル,パワースペクトルと呼ぶ.
の振幅スペクトル,位相スペクトル,パワースペクトルと呼ぶ.
- やる夫
- あれ? そういえば数学の教科書では角周波数は小文字で
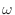 って書いてたと思うお.どうして大文字で書くんだお?
って書いてたと思うお.どうして大文字で書くんだお?
- やらない夫
- そうそう,それを説明してなかった.これまではずっと連続時間信号について話をしてきたけど,次回から離散時間信号についての話に入るんだ.つまり,時間軸上で飛び飛びの時刻にしか値をもたないような信号だな.いよいよ「ディジタル」信号処理の世界に入っていくわけだ.
離散時間信号について考えるとき,いわゆる普通の角周波数とは別に「正規化角周波数」という概念が出てくる.小文字の 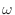 はそっちの方で使おうと思うんだ.だからそれと区別するために,普通の角周波数は
はそっちの方で使おうと思うんだ.だからそれと区別するために,普通の角周波数は 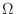 と書くことにする.ちょっと戸惑うかもしれないが,まあ我慢してくれ.
と書くことにする.ちょっと戸惑うかもしれないが,まあ我慢してくれ.
![\includegraphics[scale=0.5]{fig_ft/fs_periodic_1.eps}](img199.png)
![]() にしてみたら,どうなる?
にしてみたら,どうなる?
![\includegraphics[scale=0.5]{fig_ft/periodic_2.eps}](img201.png)
![\includegraphics[scale=0.5]{fig_ft/periodic_4.eps}](img202.png)
![\includegraphics[scale=0.5]{fig_ft/fs_periodic_2.eps}](img205.png)
![]() にしたらどうなる?
にしたらどうなる?
![\includegraphics[scale=0.5]{fig_ft/fs_periodic_4.eps}](img208.png)
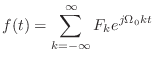
![\includegraphics[scale=0.5]{fig_ft/fs_line.eps}](img211.png)
![]() になる,ってのがフーリエ級数の意味するところだ.長さっていっても本当は複素数だという点には注意しなきゃいけないんだが,ともかくこうやって表そう.
になる,ってのがフーリエ級数の意味するところだ.長さっていっても本当は複素数だという点には注意しなきゃいけないんだが,ともかくこうやって表そう.
![\includegraphics[scale=0.5]{fig_ft/fs_rectangle.eps}](img212.png)
![\includegraphics[scale=0.5]{fig_ft/rectangle_size.eps}](img214.png)
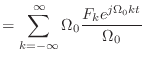
![$\displaystyle = \frac{1}{2\pi}\sum_{k=-\infty}^{\infty} \Omega_0 \frac{2\pi F_k e^{j\Omega[k] t}}{\Omega_0}$](img219.png)
![$\displaystyle = \frac{1}{2\pi}\sum_{k=-\infty}^{\infty} \Omega_0 F(\Omega[k]) e^{j\Omega[k] t}$](img222.png)
![$\displaystyle = \frac{1}{T_0} \int_{-T_0/2}^{T_0/2} f(t) e^{-j\Omega[k]t}dt$](img227.png)
![$\displaystyle = \frac{2\pi}{T_0 \Omega_0} \int_{-T_0/2}^{T_0/2} f(t) e^{-j\Omega[k]t}dt$](img230.png)
![$\displaystyle = \int_{-T_0/2}^{T_0/2} f(t) e^{-j\Omega[k]t}dt$](img231.png)
![$\displaystyle = \frac{1}{2\pi}\sum_{k=-\infty}^{\infty} F(\Omega[k]) e^{j\Omega[k] t} \Delta\Omega$](img234.png)
![]() の方も,同様に
の方も,同様に
![]() の極限を考える.単純に積分の範囲が無限大に飛んでいくだけだな.これをフーリエ変換と呼ぶ.
の極限を考える.単純に積分の範囲が無限大に飛んでいくだけだな.これをフーリエ変換と呼ぶ.
![]() と周波数変数
と周波数変数 ![]() が含まれているが,
が含まれているが,![]() で積分するから,
で積分するから,![]() だけが残る.連続時間上の関数から連続周波数上の関数への変換になるわけだ.フーリエ逆変換の方は,右辺を
だけが残る.連続時間上の関数から連続周波数上の関数への変換になるわけだ.フーリエ逆変換の方は,右辺を ![]() で積分しているから,
で積分しているから,![]() だけが残るんだな.時間関数への変換になる.
だけが残るんだな.時間関数への変換になる.
![]() をくくり出したのも,同じように単に慣例的なものなんだ.
をくくり出したのも,同じように単に慣例的なものなんだ.
![]() はそっちの方で使おうと思うんだ.だからそれと区別するために,普通の角周波数は
はそっちの方で使おうと思うんだ.だからそれと区別するために,普通の角周波数は ![]() と書くことにする.ちょっと戸惑うかもしれないが,まあ我慢してくれ.
と書くことにする.ちょっと戸惑うかもしれないが,まあ我慢してくれ.
![]() が
が ![]() のフーリエ変換であることをこんな風に表すことにする.これらは割と標準的な記法だ.
のフーリエ変換であることをこんな風に表すことにする.これらは割と標準的な記法だ.
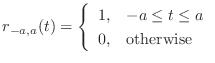
![\includegraphics[scale=0.5]{fig_ft/rectangular_func.eps}](img256.png)
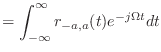
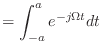
![$\displaystyle = \left[ \frac{1}{-j\Omega} e^{-j\Omega t} \right]_{-a}^{a}$](img264.png)
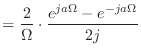
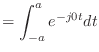
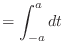
![\includegraphics[scale=0.5]{fig_ft/sinc.eps}](img276.png)
![\includegraphics[scale=0.5]{fig_ft/abs_sinc.eps}](img277.png)
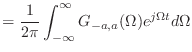
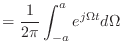
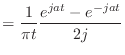
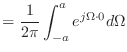
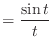
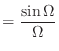
![\includegraphics[scale=0.5]{fig_ft/norm_sinc.eps}](img298.png)
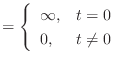
![\includegraphics[scale=0.5]{fig_ft/delta_func.eps}](img301.png)
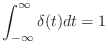
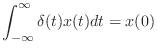
![\includegraphics[scale=0.5]{fig_ft/delta_by_x.eps}](img306.png)
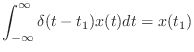
![\includegraphics[scale=0.5]{fig_ft/delta_T1_by_x.eps}](img310.png)
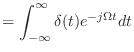
![\includegraphics[scale=0.5]{fig_ft/pair_delta.eps}](img315.png)
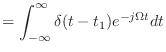
![\includegraphics[scale=0.5]{fig_ft/pair_delta_shift.eps}](img319.png)
![\includegraphics[scale=0.5]{fig_ft/time_shift.eps}](img326.png)
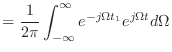
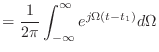
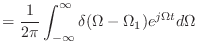
![\includegraphics[scale=0.5]{fig_ft/pair_exp.eps}](img344.png)
![]() の振動ってのは,つまり直流のことだから,
の振動ってのは,つまり直流のことだから,
![]() のところにインパルスが立つことになる.
のところにインパルスが立つことになる.
![\includegraphics[scale=0.5]{fig_ft/pair_unity.eps}](img345.png)
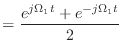
![\includegraphics[scale=0.5]{fig_ft/pair_cos.eps}](img355.png)
![]() で周期的な信号
で周期的な信号 ![]() をフーリエ変換したときにどうなるかを考えてみようか.
をフーリエ変換したときにどうなるかを考えてみようか.
![\includegraphics[scale=0.5]{fig_ft/periodic_ft_again.eps}](img357.png)
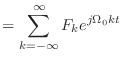
![$\displaystyle = \sum_{k=-\infty}^{\infty} F_k {\cal F}[e^{j\Omega_0 k t}]$](img359.png)
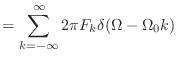
![\includegraphics[scale=0.5]{fig_ft/delta_train_F.eps}](img361.png)
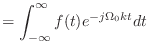
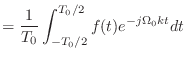
![\includegraphics[scale=0.5]{fig_ft/relation_fs_ft.eps}](img367.png)
![\includegraphics[scale=0.5]{fig_ft/relation_fs_ft_inv.eps}](img371.png)