: 10. サンプリング定理 : やる夫で学ぶディジタル信号処理 : 8. フーリエ変換の性質(2): たたみこみと積 ― 目次 アイコンを表示する
![\includegraphics[scale=0.5]{fig_parseval/inner_prod.eps}](img694.png)
で,それを周波数領域に持っていくと,もう単位が何だかわからなくなるので想像しにくくなるんだが,同じように周波数スペクトルの持つエネルギーに相当する量を右辺は表していると考えようか.時間領域の方も,実は ![]() は電圧じゃなくて全然違う次元の物理量かもしれないが,今の話からの類推で信号のエネルギーを表していると考えてしまう.そうすると,パーセバルの法則は,時間領域で表しても周波数領域で表しても,信号のエネルギーは (定数倍を除いて) 一致すると主張していることになる.
は電圧じゃなくて全然違う次元の物理量かもしれないが,今の話からの類推で信号のエネルギーを表していると考えてしまう.そうすると,パーセバルの法則は,時間領域で表しても周波数領域で表しても,信号のエネルギーは (定数倍を除いて) 一致すると主張していることになる.
![\includegraphics[scale=0.5]{fig_parseval/vector_decomp.eps}](img703.png)
![\includegraphics[scale=0.5]{fig_parseval/vector_decomp_orthonorm.eps}](img710.png)
![]() から
から ![]() の延長線上に垂線を下ろして,分解された成分の長さを決めるんだお.その成分の長さは,
の延長線上に垂線を下ろして,分解された成分の長さを決めるんだお.その成分の長さは,![]() と
と ![]() の間の角度を
の間の角度を ![]() として
として
![]() になるわけだけど,
になるわけだけど,
![]() だから,
だから,
![]() になるんだお.
になるんだお.
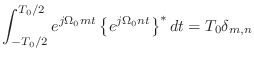 |
(2.19) |
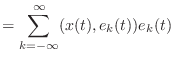 |
(9.11) |
| (9.12) | ||
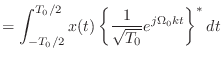 |
(9.13) | |
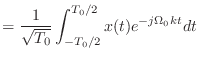 |
(9.14) |
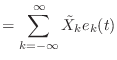 |
(9.15) | |
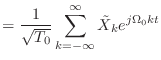 |
(9.16) |
![\includegraphics[scale=0.5]{fig_parseval/fs_orthonorm.eps}](img737.png)
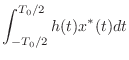 |
(9.17) |
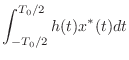 |
 |
(9.19) |
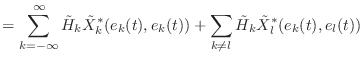 |
(9.20) |
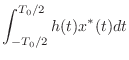 |
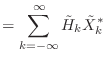 |
(9.21) |
![\includegraphics[scale=0.5]{fig_parseval/h_x_expanded.eps}](img750.png)
![\includegraphics[scale=0.5]{fig_parseval/parseval_illustrated.eps}](img752.png)
![]() とした場合の式(9.1)も同じことだが,この場合の結果は幾何学的にはもうちょっとわかりやすい.こちらも
とした場合の式(9.1)も同じことだが,この場合の結果は幾何学的にはもうちょっとわかりやすい.こちらも
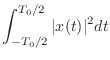 |
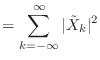 |
(9.22) |
![\includegraphics[scale=0.5]{fig_parseval/parseval_rectangular.eps}](img756.png)
例えばフーリエ変換だと,
![]() を計算しているわけだから,
を計算しているわけだから,
![]() を基底ベクトルに取っていると見ることができそうだ.周波数
を基底ベクトルに取っていると見ることができそうだ.周波数 ![]() としては全実数を取り得るから,
としては全実数を取り得るから,
![]() が基底を構成すると考えたいところだ.
が基底を構成すると考えたいところだ.
ところが,
![]() が 1 にならない,というか収束しないので,正規直交基底だと呼ぶわけにはいかない.
が 1 にならない,というか収束しないので,正規直交基底だと呼ぶわけにはいかない.
![$\displaystyle \begin{pmatrix}X[0] X[1] X[2] X[3] \end{pmatrix}$](img762.png) |
![$\displaystyle = \begin{pmatrix}W^0 & W^0 & W^0 & W^0 W^0 & W^1 & W^2 & W^3 ...
...6 & W^9 \end{pmatrix} \begin{pmatrix}x[0] x[1] x[2] x[3] \end{pmatrix}$](img763.png) |
(9.23) |
swk(at)ic.is.tohoku.ac.jp