- やらない夫
- まず,そもそも一定の長さの区間を切り出してくるっていう操作は,数式としてはこう書ける.
- やる夫
-
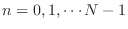 の間だけ 1 であと全部 0 になるような矩形関数をかけるんだお.
の間だけ 1 であと全部 0 になるような矩形関数をかけるんだお.
- やらない夫
- これがどうしてまずいのかというと,
 と
と  のところで
のところで
![$ w_\textnormal{r}[n]$](img888.png) の値が 0 から 1,1 から 0 に急激に変化するからだ.だから
の値が 0 から 1,1 から 0 に急激に変化するからだ.だから
![$ x[n]$](img404.png) を周期拡張したときにつながらなくなってしまう.じゃあどうするか.
を周期拡張したときにつながらなくなってしまう.じゃあどうするか.
- やる夫
- …なめらかに変化させる,ってことかお.
- やらない夫
- そういうことになるな.例えば
![$\displaystyle w_\textnormal{h}[n] = \left\{ \begin{array}{ll} \displaystyle 0.5...
...i n}{N}}, & n = 0, 1, \cdots, N-1 0, & \text{otherwise} \end{array} \right.$](img889.png) |
(11.3) |
なんていう形のものがよく使われる.
- やる夫
- 両端がなめらかに小さくなっているお.
- やらない夫
- こうやって信号の一部を切り出すためにかける関数のことを,一般に窓関数と呼ぶ.最初の
![$ w_\textnormal{r}[n]$](img888.png) は矩形窓とか方形窓とか呼ばれる.対して
は矩形窓とか方形窓とか呼ばれる.対して
![$ w_\textnormal{h}[n]$](img891.png) の方はハミング窓と呼ばれるものだ.スペクトル解析をするときは,こんな風に両端がなめらかに絞られた窓関数を使って切り出すことで,周期拡張の際につながりがおかしくなることを避けるのが重要だ.
の方はハミング窓と呼ばれるものだ.スペクトル解析をするときは,こんな風に両端がなめらかに絞られた窓関数を使って切り出すことで,周期拡張の際につながりがおかしくなることを避けるのが重要だ.
- やる夫
- うーん,でも,こんなのかけたら波形の形状が変わってしまうお.それは問題にならないのかお?
- やらない夫
- ああ,大問題だな.
- やる夫
- あっさり認めたお.
- やらない夫
- 問題だが,矩形窓を使うよりはまだましということだな.もちろんハミング窓を使うのが常に最善というわけじゃなく,他にもいろんな窓関数が提案されている.結局どうやっても何らかの形で波形は歪んでしまって,元の信号のスペクトルとは大なり小なり異なる結果が得られてしまう.そのときどきの目的に応じて都合のよい窓関数を選ぶことが重要だ.
- やる夫
- んー,一般論過ぎてピンと来ないお.具体的にはどうすればいいのかお.
- やらない夫
- そうだな.元の信号のスペクトルが,窓関数をかけることでどんな風に変化するかを考えるといい.
まず矩形窓から考えるか.
![$ w_\textnormal{r}[n]$](img888.png) の離散時間フーリエ変換
の離散時間フーリエ変換
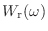 はどんな形になる?
はどんな形になる?
- やる夫
- えーと,
になるお.でもこれじゃ形はわからないお….
- やらない夫
- 連続時間の矩形関数をフーリエ変換したときのことを思い出すといいぞ.
- やる夫
- んー,あ,そうか,オイラーの公式で sin に持ち込むんだお.
ふーん,同じく矩形関数なのに,離散時間の場合は sinc 関数とは違うものになるんだお.
- やらない夫
- そうだな.振幅スペクトルの形状はこんな感じで sinc 関数に似てはいるんだが,ちょっと違う.
sinc 関数は sin の振幅が原点から離れるに従って反比例で減っていくんだったが,これは
 で減っていくんだな.しかもちゃんと周期
で減っていくんだな.しかもちゃんと周期 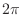 で周期的になっているのに注意しよう.
で周期的になっているのに注意しよう.
- やる夫
- あ,そうか,離散時間フーリエ変換だから,スペクトルは周期
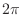 のはずなんだったお.辻褄が合ってるお.
のはずなんだったお.辻褄が合ってるお.
- やらない夫
- 時間領域で
![$ w_\textnormal{r}[n]$](img888.png) をかけるということは,周波数領域では元のスペクトルに今の形の関数
をかけるということは,周波数領域では元のスペクトルに今の形の関数
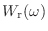 をたたみこむことになるわけだ.イメージできるか?
をたたみこむことになるわけだ.イメージできるか?
- やる夫
- そろそろ慣れてきたお.元のスペクトルの各点から,その点の高さに合わせた
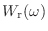 をぶら下げて,全部重ね合わせるんだお.
をぶら下げて,全部重ね合わせるんだお.
- やらない夫
- その結果どうなるかは,
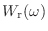 の形状の各部ごとに考えることができる.まず真ん中の大きな山の部分だな.この部分をよくメインローブと呼ぶ.たたみこまれたときに,メインローブは近傍の値同士を互いと平均化する効果を持つのがイメージできるか?
の形状の各部ごとに考えることができる.まず真ん中の大きな山の部分だな.この部分をよくメインローブと呼ぶ.たたみこまれたときに,メインローブは近傍の値同士を互いと平均化する効果を持つのがイメージできるか?
- やる夫
- ある点に
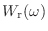 をぶら下げたときに,メインローブの分だけその点の値が広がるんだお.全部の点についてそう作用するので,確かに近傍での平均化のように作用しそうだお.
をぶら下げたときに,メインローブの分だけその点の値が広がるんだお.全部の点についてそう作用するので,確かに近傍での平均化のように作用しそうだお.
- やらない夫
- なので,例えばスペクトルに非常に近接した2本のピークがあったとすると,メインローブの影響で両者がくっついてしまったりする.本当は2本のピークがあることを見逃してしまったりしがちなわけだ.
- やる夫
- なるほど,てことはメインローブはできるだけ細い方がいいんだお.
- やらない夫
- 次にメインローブ以外の背の低い山の部分,これらはサイドローブと呼ばれる.サイドローブは,ある点の値の影響を,ずっと遠くまで引きずる効果を持つことになる.
- やる夫
- てことはどこかに大きなピークがあると,関係ないところまでちょっとずつ底上げされることになるお.
- やらない夫
- その結果,スペクトルの小さなピークが,無関係な大きなピークからの影響に埋もれてしまったりする恐れがある.だからサイドローブはできるだけ低いことが望ましい.
- やる夫
- 結局,メインローブが限りなく細くて,サイドローブが限りなく存在しない,単位インパルスみたいな形状のものをたたみこむのが一番ってことだお?
- やらない夫
- いや,そりゃそうなんだが,周波数領域で単位インパルスになるってことは時間領域では定数 1 だからな.窓をかけることにならんだろ.
- やる夫
- あ,そっか,ダメだお.
- やらない夫
- 一定の長さの窓関数として機能するものを考えている限り,すべての要件を同時に満たすのは不可能で,トレードオフの関係にある.だから,目的に応じて選択する必要があるわけだな.
で,具体例としてさっきのハミング窓のスペクトルを見てみよう.
- やる夫
- メインローブはむしろやや太くなってるお.でもサイドローブはかなり小さくなってるお.
- やらない夫
- 矩形窓は,実はメインローブの細さについてはかなりよい性能を持っている.ただしサイドローブが高すぎてまずいわけだ.時間領域との対応で考えると,矩形窓は周期拡張の境目で信号が不連続になるのが問題だった.不連続な関数を作るためには,無限に高い周波数成分まで重ね合わせてやらなくてはならない.低周波数のサイン波では滑らかな信号にしかならないからな.つまり広い周波数に渡って偽の成分が発生してしまうことになる.まさにサイドローブの効果なわけだ.
- やる夫
- ハミング窓みたいに両端を絞ってやるとその効果は抑えられるけど,波形が歪んでスペクトルの形状が変わっちゃうわけだお.メインローブの太さとか,残ったサイドローブがその効果をもたらしていることになるお.
- やらない夫
- 他の代表的な窓関数としては,ハニング窓,ブラックマン窓などがある.興味があれば調べてみるといい.
それから,ちょっと注意点だ.今回ハミング窓は周期 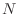 の cos と矩形関数を組み合わせたような関数で表した.教科書によっては代わりに周期
の cos と矩形関数を組み合わせたような関数で表した.教科書によっては代わりに周期 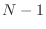 の
cos を使っている場合もある.
の
cos を使っている場合もある.
- やる夫
- んーと,それは別の窓関数にならないかお.
- やらない夫
- もちろん厳密には別の関数だし,特性も全く同じじゃないが,まあ流儀の違い程度のものだと思ってもらうのがいいかな.いずれにせよ長さ
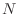 の区間の両端を絞るという目的は同じだ.
の区間の両端を絞るという目的は同じだ.
![\includegraphics[scale=0.5]{fig_win/window.eps}](img874.png)
![\includegraphics[scale=0.5]{fig_win/multi_window.eps}](img875.png)
![\includegraphics[scale=0.5]{fig_win/multi_window_overlap.eps}](img876.png)
![\includegraphics[scale=0.5]{fig_win/window_ok.eps}](img878.png)
![\includegraphics[scale=0.5]{fig_win/window_ng.eps}](img879.png)
![\includegraphics[scale=0.5]{fig_win/window_ng_repeated.eps}](img880.png)
![\includegraphics[scale=0.5]{fig_win/block_window.eps}](img881.png)
![$\displaystyle w_\textnormal{r}[n] = \left\{ \begin{array}{ll} 1, & n = 0, 1, \cdots, N-1 0, & \text{otherwise} \end{array} \right.$](img884.png)
![\includegraphics[scale=0.5]{fig_win/window_rect.eps}](img885.png)
![$\displaystyle w_\textnormal{h}[n] = \left\{ \begin{array}{ll} \displaystyle 0.5...
...i n}{N}}, & n = 0, 1, \cdots, N-1 0, & \text{otherwise} \end{array} \right.$](img889.png)
![\includegraphics[scale=0.5]{fig_win/window_hamming.eps}](img890.png)
![]() の離散時間フーリエ変換
の離散時間フーリエ変換
![]() はどんな形になる?
はどんな形になる?
![$\displaystyle = \sum_{n = -\infty}^{\infty} w_\textnormal{r}[n] e^{-j\omega n}$](img894.png)
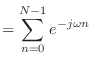
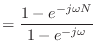
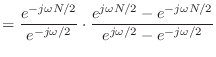
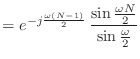
![\includegraphics[scale=0.5]{fig_win/spectre_rect.eps}](img899.png)
![]() で減っていくんだな.しかもちゃんと周期
で減っていくんだな.しかもちゃんと周期 ![]() で周期的になっているのに注意しよう.
で周期的になっているのに注意しよう.
![\includegraphics[scale=0.5]{fig_win/mainlobe.eps}](img901.png)
![\includegraphics[scale=0.5]{fig_win/sidelobe.eps}](img902.png)
![\includegraphics[scale=0.5]{fig_win/spectre_hamming.eps}](img903.png)
![]() の cos と矩形関数を組み合わせたような関数で表した.教科書によっては代わりに周期
の cos と矩形関数を組み合わせたような関数で表した.教科書によっては代わりに周期 ![]() の
cos を使っている場合もある.
の
cos を使っている場合もある.