- やる夫
- 線形位相特性を持たせることができないってことは,
IIR フィルタって使い物にならないのかお?
- やらない夫
- そんなことはないぞ.全周波数で完全に線形位相でなくても,必要な帯域でだけ近似的に線形位相と見なせれば十分な場合もあったりする.例えば周波数選択フィルタの場合,信号を通過させる帯域だけ考えれば十分なわけだ.
- やる夫
- ああ,確かに阻止される帯域の出力信号は,波形が歪んでようが大して問題じゃないお.
- やらない夫
- さらに,応用によっては,個々の周波数成分の遅延はそれほど重要じゃなく,むしろ群遅延と呼ばれるものの方が重要な場合がある.
- やる夫
- ん? どういうことだお?
- やらない夫
- 具体例で考えよう.前に,振幅変調という概念について説明したと思う.
- やる夫
- 覚えてるお.時間シフトの公式を,時間と周波数を逆にして考えたものだったお.
- やらない夫
- 時間信号
![$ x[n]$](img404.png) に
に
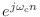 をかけると,周波数領域では
をかけると,周波数領域では
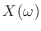 から
から
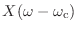 に周波数シフトするんだった.
に周波数シフトするんだった.
- やる夫
- 例えば音声信号
![$ x[n]$](img404.png) を周波数
を周波数
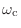 の搬送波に乗せて通信する場合なんかを表しているんだったお.
の搬送波に乗せて通信する場合なんかを表しているんだったお.
- やらない夫
- 変調された後の信号
![$ x[n] e^{j\omega_\textnormal{c}n}$](img1487.png) には,周波数
には,周波数
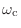 やその近くの周波数成分が含まれている.この信号を何らかのフィルタに通すとそれらの周波数成分がそれぞれ遅れて出てくることになるが,その遅延にはあまり興味はない.
やその近くの周波数成分が含まれている.この信号を何らかのフィルタに通すとそれらの周波数成分がそれぞれ遅れて出てくることになるが,その遅延にはあまり興味はない.
- やる夫
- ん? そうなのかお?
- やらない夫
- いま送ろうとしている音声信号は,変調信号の振幅の変化として表現されているわけだ.その振幅変化の波形,つまり包絡線がどのくらい遅れるかの方がずっと重要だ.
- やる夫
- あー,まあ確かにそうかも知れないお.こういう場合に搬送波の位相がどのくらい遅れているかは割とどうでもよさそうだお.
- やらない夫
- こういう状況は,通信のために変調している場合だけに限らない.例えば
440 Hz の音叉をポーンと鳴らしたときの音声信号を考えよう.このときの信号は,440 Hz のサイン波の振幅,つまり音量が,音叉を叩いた瞬間に急激に立ち上がって,その後ゆっくりと減衰していくような波形になるだろう.
- やる夫
- あー,そうか,音叉の音量変化の波形が
![$ x[n]$](img404.png) で,440 Hz のサイン波が搬送波だとすれば同じ話になるお.この場合も,フィルタを通したときに重要なのは包絡線の遅れの方で,440 Hz の振動の位相のずれの方じゃないお.
で,440 Hz のサイン波が搬送波だとすれば同じ話になるお.この場合も,フィルタを通したときに重要なのは包絡線の遅れの方で,440 Hz の振動の位相のずれの方じゃないお.
- やらない夫
- 群遅延ってのは,こういう場合に包絡線の波形がどのくらい遅れるかを表す量だ.結論から言ってしまうと,群遅延は位相特性曲線の傾きで表される.正確にいうと傾きにマイナスをつけたもの,つまり群遅延
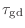 は
は
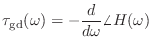 |
(15.43) |
と表すことができる.
ついでに,これまで考えてきた,各周波数成分がそれぞれどのくらい遅れるかという意味での遅れ時間
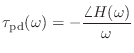 |
(15.44) |
のことを位相遅延と呼んだりする.線形位相の場合は,群遅延も位相遅延も等しい定数だ.一般にはいずれも 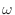 の関数になる.
の関数になる.
- やる夫
- あれ?
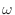 によって変わるんなら,包絡線波形の遅れ時間ってのはどの
によって変わるんなら,包絡線波形の遅れ時間ってのはどの
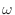 のときの値を考えればいいんだお?
のときの値を考えればいいんだお?
- やらない夫
- ああ,それは,搬送波周波数
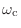 のときの値を使うことになる.
のときの値を使うことになる.
- やる夫
- ふーん,そういうもんなのかお.ていうか何故そうなるのかがわからないから,理解のしようがないお.直観的にでいいから説明してくれお.
- やらない夫
- …うーん,これに関しては直観的に説明する方がむしろ難しいな.ちゃんと数式を展開する方が説明しやすい.
- やる夫
- (あー,またヤブヘビをつついた気がするお)
- やらない夫
- 周波数
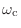 の搬送波が時間信号
の搬送波が時間信号 ![$ x[n]$](img404.png) で振幅変調されているとしよう.さっきから話している通り,そのスペクトルは
で振幅変調されているとしよう.さっきから話している通り,そのスペクトルは
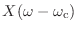 だ.
だ.
- やる夫
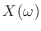 が
が
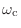 だけ周波数シフトされたんだお.
だけ周波数シフトされたんだお.
- やらない夫
- この信号をあるフィルタ
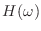 に通す.位相特性にだけ注目したいので,振幅特性は常に 1 だとしよう.位相特性は,搬送波周波数
に通す.位相特性にだけ注目したいので,振幅特性は常に 1 だとしよう.位相特性は,搬送波周波数
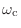 のときに
のときに
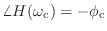 で,その周囲の
で,その周囲の
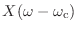 の成分が存在する範囲では傾き
の成分が存在する範囲では傾き
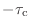 で一定と見なせるとしよう.
で一定と見なせるとしよう.
- やる夫
- えーと,
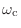 の近辺では線形位相と見なせるってことかお?
の近辺では線形位相と見なせるってことかお?
- やらない夫
- いや,そうとは限らない.位相特性の
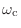 の近辺の直線部分を延長したときに原点を通るならば,確かにその通りだ.ただし今はこの範囲で「傾きが」一定だといっているだけなので,延長線が原点を通る保証は全くない.
の近辺の直線部分を延長したときに原点を通るならば,確かにその通りだ.ただし今はこの範囲で「傾きが」一定だといっているだけなので,延長線が原点を通る保証は全くない.
- やる夫
- そっか,なので,この範囲の位相遅延は必ずしも一定というわけではないんだお.
- やらない夫
- そういうことだ.それにも関わらず,包絡線の波形は歪まずに
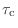 遅れるだけになることをこれから示そう.
遅れるだけになることをこれから示そう.
まず,いま着目している
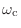 の近くの範囲で,このフィルタの周波数特性は
の近くの範囲で,このフィルタの周波数特性は
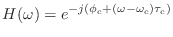 |
(15.45) |
と表せる.
- やる夫
- いきなり何かややこしいお.えーと,振幅特性が常に 1 ってのは満たしてるお.
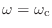 のときの位相はというと
のときの位相はというと
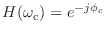 になっているのでこれも大丈夫だお.で,
になっているのでこれも大丈夫だお.で,
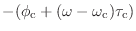 を
を
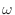 で微分したら
で微分したら
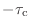 になるので,この近辺で傾きが
になるので,この近辺で傾きが
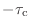 だってのも OK だお.合ってそうだお.
だってのも OK だお.合ってそうだお.
- やらない夫
- 変調信号
![$ x[n] e^{j\omega_\textnormal{c}n}$](img1487.png) をこのフィルタに通す.その出力
をこのフィルタに通す.その出力 ![$ y[n]$](img572.png) を周波数領域で見ると,
を周波数領域で見ると,
になる.
- やる夫
- うー,面倒くさそうな式だお.
- やらない夫
- 一つずつ見ていけばそうでもないぞ.まず最初の
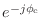 は
は
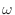 を含んでない,ただの定数倍だ.残りの部分は複雑そうに見えるが,
を含んでない,ただの定数倍だ.残りの部分は複雑そうに見えるが,
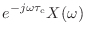 |
(15.49) |
を
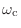 だけ周波数シフトしたものだと考えればいい.
だけ周波数シフトしたものだと考えればいい.
- やる夫
- ふーん,そう思ってみるとそんなに複雑でもなかったお.
- やらない夫
- さて,これを時間領域で見てみよう.定数倍の
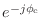 はそのままだ.
はそのままだ.
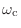 だけ周波数シフトした分は,時間領域では
だけ周波数シフトした分は,時間領域では
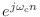 をかけることに対応する.そして,
をかけることに対応する.そして,
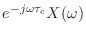 は時間シフトの公式から
は時間シフトの公式から
![$ x[n - \tau_\textnormal{c}]$](img1509.png) になる.これらをまとめると
になる.これらをまとめると
![$\displaystyle y[n] = e^{-j\phi_\textnormal{c}} e^{j\omega_\textnormal{c}n} x[n - \tau_\textnormal{c}]$](img1510.png) |
(15.50) |
という信号がフィルタから出てくることになる.
- やる夫
- あー,
![$ x[n]$](img404.png) が
が
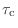 だけ遅れてるお.
だけ遅れてるお.
- やらない夫
- そこが核心だ.包絡線波形
![$ x[n]$](img404.png) を
を
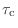 遅らせたものを搬送波
遅らせたものを搬送波
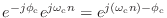 に乗せたものが出力されるということだ.搬送波の位相が
に乗せたものが出力されるということだ.搬送波の位相が
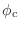 だけずれているが,そっちには興味はない.包絡線波形が群遅延
だけずれているが,そっちには興味はない.包絡線波形が群遅延
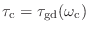 の分だけ遅れることが確認できたわけだ.
の分だけ遅れることが確認できたわけだ.
- やる夫
- …あれ? ちょっと待って欲しいお.
![$ x[n]$](img404.png) って離散時間信号なんだお?
って離散時間信号なんだお?
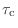 が整数じゃないときは,
が整数じゃないときは,
![$ x[n - \tau_\textnormal{c}]$](img1509.png) ってどうなるんだお?
ってどうなるんだお?
- やらない夫
- 鋭いな.その通り,
![$ x[n - \tau_\textnormal{c}]$](img1509.png) という表記は
という表記は
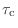 が整数のときしか意味を持たない.が,一般に群遅延は実数なので困ったことになる.
が整数のときしか意味を持たない.が,一般に群遅延は実数なので困ったことになる.
詳しい説明は省くが,こんな風に理解して欲しい.離散時間信号 ![$ x[n]$](img404.png) を,サンプリング定理のときに出てきた理想的低域通過フィルタに通して,いったん連続時間信号
を,サンプリング定理のときに出てきた理想的低域通過フィルタに通して,いったん連続時間信号
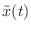 を作る.次に,これを
を作る.次に,これを
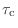 だけ遅らせた
だけ遅らせた
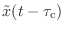 を作る.最後にこれをサンプリングし直す.このようにして得られる離散時間信号のことを
を作る.最後にこれをサンプリングし直す.このようにして得られる離散時間信号のことを
![$ x[n - \tau_\textnormal{c}]$](img1509.png) という記法で表すと約束することにしよう.
という記法で表すと約束することにしよう.
- やる夫
- んー,つまり
![$ x[n]$](img404.png) を,何か背後にある連続時間信号をサンプリングしたものだと考えて,遅延させる必要があるときはその連続時間信号の方を遅延させるって話になるお.天下りの説明だからちゃんとは理解できないけど,辻褄は合ってそうな気がするお.
を,何か背後にある連続時間信号をサンプリングしたものだと考えて,遅延させる必要があるときはその連続時間信号の方を遅延させるって話になるお.天下りの説明だからちゃんとは理解できないけど,辻褄は合ってそうな気がするお.
- やらない夫
- ちゃんと理解したかったら,今のような手順で遅延させた信号のスペクトルと,元の信号のスペクトルに
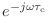 をかけたものとが一致することを計算で確かめてみるといい.
をかけたものとが一致することを計算で確かめてみるといい.
さて,また長くなりそうなので,この辺で切り上げてまとめよう.
- ディジタルフィルタの周波数選択特性は,周波数特性 (= 周波数応答) のうち特に振幅特性 (= 振幅応答) を調べることで把握できる.
- 周波数
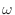 の単振動は,振幅が
の単振動は,振幅が
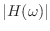 倍されて出力される.
倍されて出力される.
- 位相特性 (= 位相応答) を調べることで,入力信号がどのくらい遅れて出てくるかを把握できる.
-
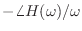 を位相遅延といい,周波数
を位相遅延といい,周波数  の単振動がどのくらい遅れて出力されるかを表す.
の単振動がどのくらい遅れて出力されるかを表す.
-
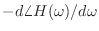 を群遅延といい,周波数
を群遅延といい,周波数 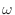 の搬送波を振幅変調した際の包絡線波形がどのくらい遅れて出力されるかを表す.
の搬送波を振幅変調した際の包絡線波形がどのくらい遅れて出力されるかを表す.
- 位相遅延 = 群遅延 = 一定 であるような特性を線形位相特性と呼ぶ.線形位相特性を持つにはインパルス応答が左右対称な形状をしていなくてはならず,したがって因果的な IIR フィルタは線形位相特性を持ち得ない.
- 伝達関数の極と零点の配置を考えることで,フィルタの大まかな特性を把握できる.
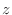 領域の単位円の近くに零点があれば,振幅特性はその偏角の周波数の付近で小さくなる.特に単位円上に零点があるなら,その周波数で振幅特性が 0 になる.
領域の単位円の近くに零点があれば,振幅特性はその偏角の周波数の付近で小さくなる.特に単位円上に零点があるなら,その周波数で振幅特性が 0 になる.
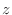 領域の単位円の近くに極があれば,振幅特性はその偏角の周波数の付近で大きくなる.
領域の単位円の近くに極があれば,振幅特性はその偏角の周波数の付近で大きくなる.
- 入力が有界である限り出力も有界でことが保証されるフィルタは BIBO 安定であるという.
- FIR フィルタは常に安定である.
- 因果的なフィルタが BIBO 安定であるための必要十分条件は,すべての極が単位円の内側にあることである.
- 不安定なフィルタの伝達関数
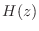 に
に
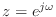 を代入して形式的に
を代入して形式的に
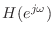 を求めても,周波数応答にはならない.
を求めても,周波数応答にはならない.
![$\displaystyle h[n] = \left\{\begin{array}{ll} \frac{1}{5}, & n = 0, 1, 2, 3, 4 0, & \text{otherwise} \end{array}\right.$](img1354.png)
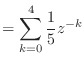
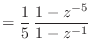
![$\displaystyle = \sum_{k = 0}^{\infty} h[k] x[n - k]$](img1357.png)
![$\displaystyle = \sum_{k = 0}^{4} \frac{1}{5} x[n - k]$](img1358.png)
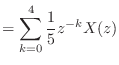
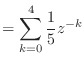
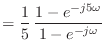
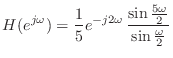
![\includegraphics[scale=0.5]{fig_dfanalysis/fir_mag.eps}](img1368.png)
![]() の場合:
の場合:
![\includegraphics[scale=0.5]{fig_dfanalysis/fir_1_10.eps}](img1371.png)
![]() の場合:
の場合:
![\includegraphics[scale=0.5]{fig_dfanalysis/fir_1_5.eps}](img1373.png)
![]() の場合:
の場合:
![\includegraphics[scale=0.5]{fig_dfanalysis/fir_2_5.eps}](img1374.png)
![]() の場合:
の場合:
![\includegraphics[scale=0.5]{fig_dfanalysis/fir_3_5.eps}](img1376.png)
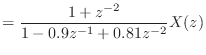
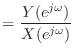
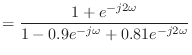
![\includegraphics[scale=0.5]{fig_dfanalysis/iir_mag.eps}](img1382.png)
![]() の場合:
の場合:
![\includegraphics[scale=0.5]{fig_dfanalysis/iir_1_10.eps}](img1383.png)
![]() の場合:
の場合:
![\includegraphics[scale=0.5]{fig_dfanalysis/iir_1_3.eps}](img1385.png)
![]() の場合:
の場合:
![\includegraphics[scale=0.5]{fig_dfanalysis/iir_1_2.eps}](img1387.png)
![]() の場合:
の場合:
![\includegraphics[scale=0.5]{fig_dfanalysis/iir_3_5.eps}](img1388.png)
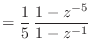
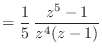
![]() を極座標で表して
を極座標で表して
![]() とすると
とすると
![\includegraphics[scale=0.5]{fig_dfanalysis/fir_pz.eps}](img1400.png)
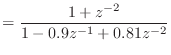
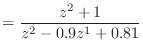
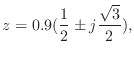
![\includegraphics[scale=0.5]{fig_dfanalysis/iir_pz.eps}](img1407.png)
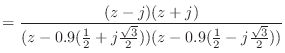
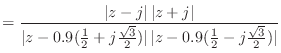
![\includegraphics[scale=0.5]{fig_dfanalysis/mag_from_pz.eps}](img1418.png)
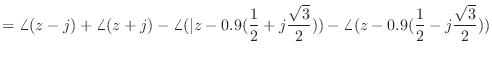
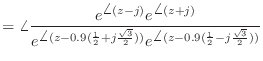
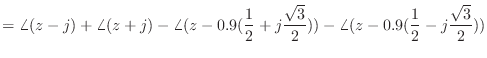
![\includegraphics[scale=0.5]{fig_dfanalysis/phase_from_pz.eps}](img1430.png)
![\includegraphics[scale=0.5]{fig_dfanalysis/iir_unstable_mag.eps}](img1437.png)
![]() の場合:
の場合:
![\includegraphics[scale=0.5]{fig_dfanalysis/iir_unstable_1_10.eps}](img1438.png)
![]() の場合:
の場合:
![\includegraphics[scale=0.5]{fig_dfanalysis/iir_unstable_1_3.eps}](img1439.png)
![$\displaystyle {\cal Z}[h[n]] = \sum_{n = 0}^{\infty} 1.2^n z^{-n}$](img1441.png)
![$\displaystyle \sum_{n = -\infty}^{\infty} \vert h[n]\vert < \infty$](img1447.png)
![]() にあるので単位円外だ.つまりこのシステムは BIBO 安定ではない.
にあるので単位円外だ.つまりこのシステムは BIBO 安定ではない.
![\includegraphics[scale=0.5]{fig_dfanalysis/iir_unstable_pz.eps}](img1463.png)
![\includegraphics[scale=0.5]{fig_dfanalysis/s_z_stable_region.eps}](img1468.png)
![]() であるシステムを考えよう.インパルス応答を離散時間フーリエ変換したものが周波数特性
であるシステムを考えよう.インパルス応答を離散時間フーリエ変換したものが周波数特性 ![]() だ.このシステムが零位相特性を持つとはどういうことだろう?
だ.このシステムが零位相特性を持つとはどういうことだろう?
![\includegraphics[scale=0.5]{fig_dfanalysis/h_symmetric.eps}](img1470.png)
![\includegraphics[scale=0.5]{fig_dfanalysis/h_symmetric_shift.eps}](img1475.png)
![]() に
に
![]() をかけて
をかけて
![]() という周波数特性を持つことになる.このような特性のことを,線形位相特性と呼ぶ.
という周波数特性を持つことになる.このような特性のことを,線形位相特性と呼ぶ.
![\includegraphics[scale=0.5]{fig_dfanalysis/linear_phase.eps}](img1480.png)
![\includegraphics[scale=0.5]{fig_dfanalysis/mod_time.eps}](img1484.png)
![\includegraphics[scale=0.5]{fig_dfanalysis/mod_freq.eps}](img1485.png)
![\includegraphics[scale=0.5]{fig_dfanalysis/delay_envelope.eps}](img1488.png)
![\includegraphics[scale=0.5]{fig_dfanalysis/tone_burst.eps}](img1489.png)
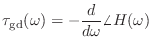
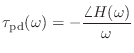
![\includegraphics[scale=0.5]{fig_dfanalysis/phase_group_delay.eps}](img1493.png)
![\includegraphics[scale=0.5]{fig_dfanalysis/group_delay_slope.eps}](img1496.png)
![]() の近くの範囲で,このフィルタの周波数特性は
の近くの範囲で,このフィルタの周波数特性は
![]() を,サンプリング定理のときに出てきた理想的低域通過フィルタに通して,いったん連続時間信号
を,サンプリング定理のときに出てきた理想的低域通過フィルタに通して,いったん連続時間信号
![]() を作る.次に,これを
を作る.次に,これを
![]() だけ遅らせた
だけ遅らせた
![]() を作る.最後にこれをサンプリングし直す.このようにして得られる離散時間信号のことを
を作る.最後にこれをサンプリングし直す.このようにして得られる離散時間信号のことを
![]() という記法で表すと約束することにしよう.
という記法で表すと約束することにしよう.