- やらない夫
- ディジタルフィルタについていろいろと考えてきたわけだが,要するに,フィルタの伝達関数が与えられれば周波数特性とか安定性とかいった特性を知ることができるってことだった.
で,いよいよその逆の話だ.望ましい周波数特性が与えられたときに,そのような特性を実現するフィルタはどうやって作ればいいかという問題を考える.フィルタの設計問題ってやつだな.
- やる夫
- んー,そんな改まって考えなきゃいけない話かお? 周波数特性
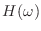 が与えられてるんだから,離散時間逆フーリエ変換すればインパルス応答
が与えられてるんだから,離散時間逆フーリエ変換すればインパルス応答
![$ h[n]$](img589.png) がわかるお.で,それをたたみこむ
がわかるお.で,それをたたみこむ
![$ y[n] = h[n] * x[n]$](img1311.png) ってフィルタを作ればそれで終わりだお.簡単な話だお?
ってフィルタを作ればそれで終わりだお.簡単な話だお?
- やらない夫
- そう思うなら実際に具体例を計算してみようか.最も基本的なものってことで,理想的低域通過フィルタ
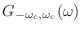 |
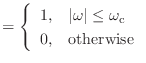 |
(16.1) |
を考えよう.周波数
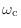 以下の低域は完全に通すが,それより上の周波数は完全に遮断する.周波数特性が常に実数値を取っているので零位相特性になっている.
以下の低域は完全に通すが,それより上の周波数は完全に遮断する.周波数特性が常に実数値を取っているので零位相特性になっている.
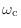 のことを遮断周波数とか,カットオフ周波数とか呼んだりする.ディジタルフィルタを考えているので,角周波数としては
のことを遮断周波数とか,カットオフ周波数とか呼んだりする.ディジタルフィルタを考えているので,角周波数としては 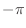 〜
〜 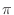 の範囲しか考えないことに注意しておこう.遮断周波数は
の範囲しか考えないことに注意しておこう.遮断周波数は
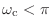 の値のみ取れるってことだな.
の値のみ取れるってことだな.
- やる夫
- 離散時間逆フーリエ変換してみるお.
ってなるから,あ,なんだ,計算上は式 (3.31) で計算した逆フーリエ変換と一緒だお.あのときの 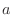 が
が
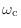 になって,
になって,
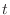 は
は 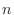 になるだけだから結局
になるだけだから結局
![$\displaystyle {\text{DTFT}^{-1}}[G_{-\omega_\textnormal{c},\omega_\textnormal{c}}(\omega)]$](img1523.png) |
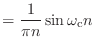 |
(16.4) |
になるお.
- やらない夫
- sinc 関数を離散化したものだな.グラフはこんな形だった.本当は離散的に描かないといけないが,面倒なので連続的に描いている.以下同様だ.
さて考えてほしいんだが,これをどうやって実際にたたみこむ?
- やる夫
- どうやってって,そんなもん公式通りたたみこめばいいんだお.
…あ,そうか,無限に総和とらなきゃならないお.
- やらない夫
- その通り.だから有限の時間では計算できない.ついでに言っておくと,sinc
関数は時刻が負のときも値を持っている.つまりこのフィルタは 因果的ではない.
- やる夫
- あー,てことは,仮に無限の計算能力を持っていたとしても,リアルタイムに動作するフィルタとしては動かせないんだお.ていうか,よく考えるとそもそも零位相特性の因果的フィルタは作れないんだったから当たり前だお.
- やらない夫
- といった辺りが最初の疑問に対する答えだ.周波数特性を単純に離散時間逆フーリエ変換しても,物理的に実行可能なフィルタが得られるとは限らないし,まあ普通はそううまくいかない.
- やる夫
- じゃあどうすればいいんだお?
- やらない夫
- それが今回の話題なわけだが,具体的な方法は,それこそ数え切れないほど提案されている.そのうち本当に基本的なものだけを簡単に説明していこうと思う.
- やる夫
- やらない夫の言う「簡単に」は信用できないお.
- やらない夫
- …ああ,確かにそうかも知れん.
- やる夫
- 否定して欲しかったお.
- やらない夫
- 基本的なものといっても,いくつかの方針に分かれる.最初の,そしておそらく最大の分かれ目は,FIR にするか IIR にするかだ.
- やる夫
- えーと,インパルス応答が有限で終わるか,無限に続くかだったお.
- やらない夫
- さっきの理想的低域通過フィルタの例でいくと,本来は無限に続くインパルス応答を何とか誤魔化して有限で打ち切ると FIR フィルタになる.結果として得られるフィルタ特性は,もちろん本来欲しかったものとは多かれ少なかれ異なったものになる.
- やる夫
- 同じ打ち切るんでも,できるなら長く取る方が本来の特性には近づけられそうだお.
- やらない夫
- 基本的にはその通りだ.FIR フィルタってのは時間領域の差分方程式で
あるいは伝達関数で表すなら
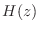 |
![$\displaystyle = \sum_{n=0}^{M} h[n]z^{-n}$](img1531.png) |
(16.7) |
と書けたわけだが,この定数 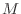 をフィルタの次数という.次数が大きいほど打ち切りの影響は小さくできる.しかしその分,過去の入力値
をフィルタの次数という.次数が大きいほど打ち切りの影響は小さくできる.しかしその分,過去の入力値 ![$ x[n - m]$](img1532.png) をたくさん記憶しておかないといけなくなるし,もちろん計算量も増える.それに,初期状態から始めてフィルタが定常的な状態になるまでに長い時間がかかるようになる.
をたくさん記憶しておかないといけなくなるし,もちろん計算量も増える.それに,初期状態から始めてフィルタが定常的な状態になるまでに長い時間がかかるようになる.
- やる夫
- ていうことは,できるだけ次数は小さく取りたいわけだお.でもそうすると特性が要求仕様からずれてってしまうお.
- やらない夫
- なので,特性をどのくらいまでなら妥協できるかを明確にしておくことが重要だ.妥協できる範囲でできるだけ小さな次数を選ぶ.
- やる夫
- インパルス応答を有限で打ち切るから妥協が必要なんだお?
じゃあ,IIR フィルタならインパルス応答を打ち切らなくていいんじゃないかお?
- やらない夫
- 打ち切る必要はないが,だからといって所望のインパルス応答を必ず表現できるわけじゃない.IIR フィルタは差分方程式で
あるいは伝達関数で表して
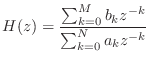 |
(16.8) |
と書けるわけだが,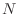 や
や 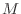 が有限じゃないとやっぱり実行できない.
が有限じゃないとやっぱり実行できない.
- やる夫
- あー,IIR フィルタのインパルス応答が無限に続くからといって,無限に続くどんなインパルス応答でも実現できるというわけじゃないんだお.
- やらない夫
- 次数が小さいとやっぱり表現できるインパルス応答の自由度が小さいので,仕様として与えられた特性そのものを実現するのは難しくなる.その辺の事情は
FIR フィルタと同じだ.
- やる夫
- やっぱり妥協が必要だってことだお.でも,具体的にどんな点を妥協をすればいいんだお?
- やらない夫
- そうだな,ざっくり言うと2点ある.1つめは遮断特性だ.理想的なフィルタ特性では,遮断周波数の前後で「完全に通過」「完全に阻止」としたいわけだが,後で見るように実際には「通過域」から「阻止域」まで徐々に振幅特性が落ちていく区間が発生してしまう.フィルタの次数が小さいと,この区間を小さくするのが難しい.遮断特性を急峻にしにくいという言い方をする.
- やる夫
- ふーん,つまり遮断特性が鈍るのをどのくらいまで許容できるかってのが第 1
の妥協点になるわけだお.
- やらない夫
- 2つめはリップル特性と呼ばれるものだ.理想的には,通過域では振幅を完全に 1
に,阻止域では完全に 0 にしたい.しかし実際には,これも後で実例を見るが,振幅が波打ってしまったりする.この振幅の波のことをリップルと呼んでいる.あるいは,リップルの振幅の大きさのことをリップルと呼ぶ場合もある.
- やる夫
- リップルも小さい方が嬉しいけど,どのくらいまで発生してもいいかってのが妥協点になるわけだお.
- やらない夫
- フィルタの仕様に関する用語をまとめておこう.低域通過フィルタの場合だけ説明するが,ほかのフィルタでも同じように使う.
通過域と阻止域それぞれで許容できるリップルの大きさを,それぞれ許容通過域リップル,許容阻止域リップルと呼ぶ.で,今まで通過域とか阻止域とかをちゃんと定義せずに使ってきたが,振幅の変動が許容通過域リップル内に収まっている帯域が通過域だ.同じように,許容阻止域リップル内に収まっている帯域を阻止域と呼ぶことにする.残った部分が遷移域ということになる.
- やる夫
- 遷移域で徐々に振幅が落ちていくと,遮断周波数って曖昧にならないかお?
- やらない夫
- 曖昧だと困るので,普通は「振幅の2乗が半分になる周波数」と定めることが多い.「振幅が
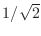 倍になる周波数」と言い換えてもいい.
倍になる周波数」と言い換えてもいい.
- やる夫
- つまり,こういう遮断特性とかリップル特性とかをどのくらい妥協できるかを考えて,その範囲でできるだけ次数の小さいフィルタを作ろうってことだお.
- やらない夫
- そういうことになるな.もちろん,FIR なのか IIR なのかとか,どういう設計法を使うのかとかによってそれらの特性への影響も変わってくるので,それぞれのケースでよく考える必要がある.
- やる夫
- んー,そういえば,FIR にするか IIR にするかが大きな分かれ目だっていう話の途中だったお.いまだにその決め手がわからないままだお.
- やらない夫
- 後で実例を見たときに確認して欲しいんだが,大雑把に言うと,同じ次数なら IIR フィルタの方が FIR フィルタよりも急峻な遮断特性を得やすい.なので,その点では IIR フィルタの方が有利だ.
- やる夫
- じゃあ FIR フィルタなんて必要ないのかお?
- やらない夫
- そんなことないぞ.前回の話を思い出して欲しいんだが,IIR フィルタには線形位相特性を持たせることが絶対にできない.だから,線形位相特性が必要なときは FIR フィルタを選ばざるを得ない.
- やる夫
- あー,そうか,波形が歪まないことが重要な場合は FIR フィルタを使うことになるわけだお.
- やらない夫
- そのほかにも,FIR フィルタが常に安定だという点が設計上の利便性につながる場合があったりとか,数値計算上の誤算の影響も FIR の方が受けにくかったりとか,いろいろな事情が FIR フィルタを選ぶ理由になる.まあその辺の詳しい話は教科書で勉強してもらうとして,以降では FIR フィルタ,IIR フィルタのごく基本的な設計法を紹介しようと思う.
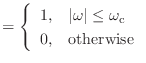
![\includegraphics[scale=0.5]{fig_dfdesign/gomegac.eps}](img1521.png)
![]() のことを遮断周波数とか,カットオフ周波数とか呼んだりする.ディジタルフィルタを考えているので,角周波数としては
のことを遮断周波数とか,カットオフ周波数とか呼んだりする.ディジタルフィルタを考えているので,角周波数としては ![]() 〜
〜 ![]() の範囲しか考えないことに注意しておこう.遮断周波数は
の範囲しか考えないことに注意しておこう.遮断周波数は
![]() の値のみ取れるってことだな.
の値のみ取れるってことだな.
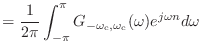
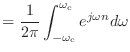
![\includegraphics[scale=0.5]{fig_dfdesign/discrete_sinc.eps}](img1527.png)
![$\displaystyle = \left\{\frac{1}{\pi n} \sin{\omega_\textnormal{c}n}\right\} * x[n]$](img1528.png)
![$\displaystyle = \sum_{m = -\infty}^{\infty} \left\{\frac{1}{\pi m} \sin{\omega_\textnormal{c}m}\right\} x[n - m]$](img1529.png)
![$\displaystyle = \sum_{m=0}^{M} h[m]x[n - m],$](img1530.png)
![$\displaystyle = \sum_{n=0}^{M} h[n]z^{-n}$](img1531.png)
![$\displaystyle \sum_{k = 0}^{N} a_k y[n - k]$](img943.png)
![$\displaystyle = \sum_{k = 0}^{M} b_k x[n - k]$](img944.png)
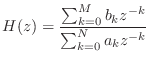
![\includegraphics[scale=0.5]{fig_dfdesign/transit.eps}](img1534.png)
![\includegraphics[scale=0.5]{fig_dfdesign/ripple.eps}](img1535.png)
![\includegraphics[scale=0.5]{fig_dfdesign/df_spec.eps}](img1536.png)
![\includegraphics[scale=0.5]{fig_dfdesign/ideal_mag_imp.eps}](img1539.png)
![\includegraphics[scale=0.5]{fig_dfdesign/sinc_truncated.eps}](img1541.png)
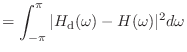
![$\displaystyle \sum_{n=-\infty}^{\infty} \vert h_\textnormal{d}[n] - h[n] \vert^...
...i} \int_{-\pi}^{\pi} \vert H_\textnormal{d}(\omega) - H(\omega) \vert^2 d\omega$](img1555.png)
![$\displaystyle = 2\pi \sum_{n = -\infty}^{\infty} \vert h_\textnormal{d}[n] - h[n] \vert^2$](img1556.png)
![$\displaystyle = 2\pi\sum_{\vert n\vert \leq L} \vert h_\textnormal{d}[n] - h[n] \vert^2 + 2\pi\sum_{\vert n\vert > L} \vert h_\textnormal{d}[n] - h[n] \vert^2$](img1557.png)
![$\displaystyle = 2\pi\sum_{\vert n\vert \leq L} \vert h_\textnormal{d}[n] - h[n] \vert^2 + 2\pi\sum_{\vert n\vert > L} \vert h_\textnormal{d}[n] \vert^2$](img1558.png)
![\includegraphics[scale=0.5]{fig_dfdesign/sinc_shifted.eps}](img1563.png)
![\includegraphics[scale=0.5]{fig_dfdesign/fir_rect.eps}](img1566.png)
![\includegraphics[scale=0.5]{fig_win/spectre_rect.eps}](img899.png)
![\includegraphics[scale=0.5]{fig_dfdesign/fir_hamming.eps}](img1568.png)
![\includegraphics[scale=0.5]{fig_dfdesign/bw_poles.eps}](img1574.png)
![\includegraphics[scale=0.5]{fig_dfdesign/bw_mag.eps}](img1576.png)
![]() の式で表すことができる.そういう
の式で表すことができる.そういう ![]() の式を,
の式を,![]() の式にうまいこと変換しようという話の流れになる.一般に,変換の元となるアナログフィルタのことをプロトタイプフィルタとか呼んだりする.プロトタイプってのは「原型」ってことだな.
の式にうまいこと変換しようという話の流れになる.一般に,変換の元となるアナログフィルタのことをプロトタイプフィルタとか呼んだりする.プロトタイプってのは「原型」ってことだな.
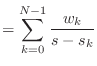
![$\displaystyle = u_0[n] \sum_{k = 0}^{N-1} w_k e^{s_k n}$](img1580.png)
![$\displaystyle = u_0[n] \sum_{k = 0}^{N-1} w_k (e^{s_k})^n$](img1581.png)
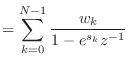
![\includegraphics[scale=0.5]{fig_dfdesign/impinvar_alias.eps}](img1585.png)
![\includegraphics[scale=0.5]{fig_dfdesign/iir_impinvar.eps}](img1587.png)
![]() のときがわかりやすいかな.
のときがわかりやすいかな.
![]() で折り返された結果,遮断域で振幅が下がりにくくなっている.
で折り返された結果,遮断域で振幅が下がりにくくなっている.
![\includegraphics[scale=0.5]{fig_dfdesign/bilinear_mapping.eps}](img1590.png)
![]() だとすると,その周波数特性は
だとすると,その周波数特性は
![]() を代入して
を代入して
![]() と書ける.一方,式 (16.27) で変数変換して作ったディジタルフィルタの伝達関数は
と書ける.一方,式 (16.27) で変数変換して作ったディジタルフィルタの伝達関数は
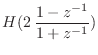
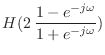
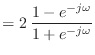
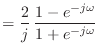
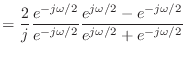
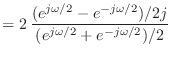
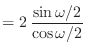
![\includegraphics[scale=0.5]{fig_dfdesign/omega_vs_omega.eps}](img1605.png)
![\includegraphics[scale=0.5]{fig_dfdesign/iir_bilinear.eps}](img1607.png)