: 15. ディジタルフィルタの解析 : やる夫で学ぶディジタル信号処理 : 13. ラプラス変換 目次 アイコンを表示する
| DTFT |
![$\displaystyle = \sum_{n = 0}^{\infty} x[n] e^{-cn} e^{-j\omega n}$](img1209.png) |
(14.1) |
![$\displaystyle = \sum_{n = 0}^{\infty} x[n] e^{-(c + j\omega) n}$](img1210.png) |
(14.2) |
![$\displaystyle {\cal L}\left[ x(t) \sum_{n = -\infty}^{\infty} \delta(t - n)\right]$](img1214.png) |
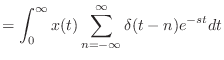 |
(14.4) |
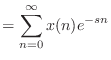 |
(14.5) |
| (14.6) | ||
| (14.7) |
ちょっといくつか簡単なものの計算をしてみるか.
| (14.8) | ||
![$\displaystyle = \sum_{n = 0}^{\infty} x[n] z^{-n}$](img1213.png) |
(14.9) | |
| (14.10) |
| (14.11) |
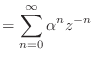 |
(14.12) | |
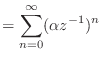 |
(14.13) | |
| (14.14) |
![\includegraphics[scale=0.5]{fig_zt/z_gt_alpha.eps}](img1243.png)
3つめ,最後の例だ.
| (14.15) |
![$\displaystyle = \sum_{n = 0}^{\infty} \delta[n] z^{-n}$](img1245.png) |
(14.16) | |
| (14.17) | ||
| (14.18) |
![\includegraphics[scale=0.5]{fig_zt/s_z_omega_const.eps}](img1252.png)
じゃあ ![]() だけが変化するとどうだ?
だけが変化するとどうだ?
![\includegraphics[scale=0.5]{fig_zt/s_z_c_const.eps}](img1256.png)
このうち特に ![]() のとき,つまり
のとき,つまり ![]() 領域の虚軸に対応するのは,
領域の虚軸に対応するのは,![]() 領域の単位円になる.
領域の単位円になる.![]() だからな.
だからな.
![\includegraphics[scale=0.5]{fig_zt/s_z_c_zero.eps}](img1258.png)
![\includegraphics[scale=0.5]{fig_zt/s_z_lines.eps}](img1259.png)
![\includegraphics[scale=0.5]{fig_zt/s_z_roc.eps}](img1260.png)
こんな風に,![]() と
と ![]() の対応関係を把握しておくことは重要だ.
の対応関係を把握しておくことは重要だ.
z 変換を導入したときの元々の関係は
| (14.19) |
| (14.20) |
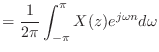 |
(14.21) |
 |
(14.23) | |
 |
(14.24) | |
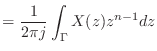 |
(14.25) |
![\includegraphics[scale=0.5]{fig_zt/izt_integral.eps}](img1274.png)
というわけで得られた式 (14.25) が逆 z 変換の公式だ.![]() じゃなくて
じゃなくて
![]() にしか戻らないというのもラプラス逆変換と同じだな.
にしか戻らないというのもラプラス逆変換と同じだな.
![$\displaystyle \sum_{k = 0}^{N} a_k y[n - k]$](img943.png) |
![$\displaystyle = \sum_{k = 0}^{M} b_k x[n - k]$](img944.png) |
(12.15) |
| (14.26) |
![$\displaystyle \sum_{k = 0}^{N} a_k D^k y[n]$](img1281.png) |
![$\displaystyle = \sum_{k = 0}^{M} b_k D^k x[n]$](img1282.png) |
(14.27) |
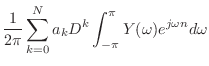 |
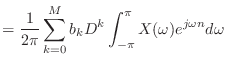 |
(14.28) |
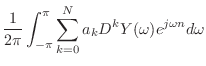 |
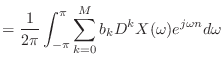 |
(14.29) |
| (14.30) | ||
| (14.31) |
![$\displaystyle \frac{1}{2\pi} \int_{-\pi}^{\pi} \left[ \sum_{k = 0}^{N} a_k (e^{-j\omega})^k Y(\omega) \right] e^{j\omega n} d\omega$](img1292.png) |
![$\displaystyle = \frac{1}{2\pi} \int_{-\pi}^{\pi} \left[ \sum_{k = 0}^{M} b_k (e^{-j\omega})^k X(\omega) \right] e^{j\omega n} d\omega$](img1293.png) |
(14.32) |
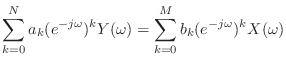 |
(14.33) |
| (14.34) | ||
| (14.35) |
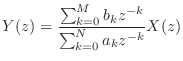 |
(14.38) |
じゃあ,これらを使って,具体例を逆 z 変換してみるか.
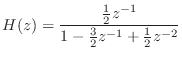 |
(14.40) |
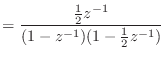 |
(14.41) |
| (14.42) |
| (14.43) | ||
| (14.44) |
そう限定すると,必ず
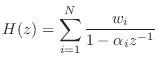 |
(14.45) |
| (14.46) |
| (14.47) |
各サブシステムの時間領域の挙動は ![]() の値で決まる.例えば
の値で決まる.例えば
![]() だったら発散するし,
だったら発散するし,
![]() なら減衰していく.複素数なら振動するって具合だ.
なら減衰していく.複素数なら振動するって具合だ.
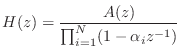 |
(14.48) |
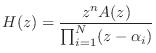 |
(14.49) |
というわけで今回のまとめだ.
swk(at)ic.is.tohoku.ac.jp