: 14. z 変換 : やる夫で学ぶディジタル信号処理 : 12. ディジタルフィルタの基礎 目次 アイコンを表示する
| (13.3) | ||
| (13.4) | ||
 |
 |
(13.5) |
| (13.6) | ||
| (13.7) | ||
| (13.8) |
| (13.9) | ||
 |
(13.10) |
 |
(13.11) |
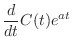 |
(13.12) | |
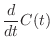 |
(13.13) | |
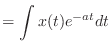 |
(13.14) |
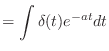 |
(13.15) |
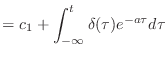 |
(13.16) | |
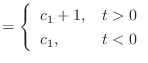 |
(13.17) |
場合分けが見苦しいので,この「デルタ関数の積分」に記号を与えて
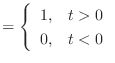 |
(13.18) |
| (13.19) |
| (13.20) |
| (13.21) | ||
| (13.22) | ||
| (13.23) |
| (13.26) | ||
| (13.27) |
式 (13.2) の微分方程式を解く場合は,まず両辺をラプラス変換するんだったな.
![$\displaystyle {\cal L}\left[ \frac{d}{dt}y(t) \right]$](img1004.png) |
(13.28) |
![$\displaystyle {\cal L}\left[ \frac{d}{dt}y(t) \right]$](img1004.png) |
(13.29) |
| (13.30) |
| (13.31) | ||
| (13.32) |
| (13.33) |
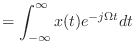 |
(13.34) |
![\includegraphics[scale=0.5]{fig_laplace/exp_a_minus_c.eps}](img1029.png)
![\includegraphics[scale=0.5]{fig_laplace/exp_a_minus_c_u0.eps}](img1032.png)
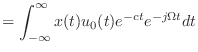 |
(13.35) | |
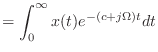 |
(13.36) |
![\includegraphics[scale=0.5]{fig_laplace/lt_fixed_c.eps}](img1037.png)
一般には ![]() の選び方に自由度があるから,移される先の直線はある程度自由に選ぶことができる.
の選び方に自由度があるから,移される先の直線はある程度自由に選ぶことができる.
![\includegraphics[scale=0.5]{fig_laplace/free_c.eps}](img1038.png)
こうして可能な限り ![]() を動かしてやった全体を考えた結果,
を動かしてやった全体を考えた結果,
![]() が複素平面上で定義されるようになって,
が複素平面上で定義されるようになって,
![]() を複素数
を複素数 ![]() の関数と捉えられることになるわけだ.
の関数と捉えられることになるわけだ.
変換された変数 ![]() の側の領域を,フーリエ変換同様に周波数領域と呼ぶ場合もあるし,複素領域とか
の側の領域を,フーリエ変換同様に周波数領域と呼ぶ場合もあるし,複素領域とか ![]() 領域とか呼ぶ場合もある.ただし,
領域とか呼ぶ場合もある.ただし,![]() はラプラス変換が収束するようにとってやる必要があるので,
はラプラス変換が収束するようにとってやる必要があるので,![]() が常に複素平面全体を動けるとは限らない点には注意が必要だ.
が常に複素平面全体を動けるとは限らない点には注意が必要だ.
![\includegraphics[scale=0.5]{fig_laplace/roc.eps}](img1042.png)
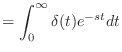 |
(13.37) | |
| (13.38) | ||
| (13.39) |
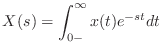 |
(13.40) |
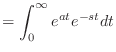 |
(13.41) | |
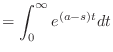 |
(13.42) | |
![$\displaystyle = \left[ \frac{1}{a - s} e^{(a - s)t} \right]_0^{\infty}$](img1050.png) |
(13.43) | |
| (13.44) |
| (13.45) | ||
| (13.46) |
| (13.47) |
| (13.48) | ||
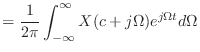 |
(13.49) |
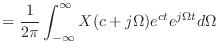 |
(13.50) | |
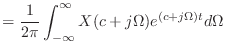 |
(13.51) |
それからもう一つ,後々のために,このラプラス逆変換の公式を直観的に理解しておいてもらいたいと思う.
![\includegraphics[scale=0.5]{fig_laplace/superpos_ft.eps}](img1076.png)
でも,
![]() の場合,どういうイメージを持てばいいのかお?
の場合,どういうイメージを持てばいいのかお?
![\includegraphics[scale=0.5]{fig_laplace/superpos_lt.eps}](img1080.png)
じゃあ,最初から
![]() で発散するような振動を重ね合わせの構成要素としておけば,重ね合わせ係数を有限で抑えることができるようになるんじゃないか.これがラプラス変換の発想だな.
で発散するような振動を重ね合わせの構成要素としておけば,重ね合わせ係数を有限で抑えることができるようになるんじゃないか.これがラプラス変換の発想だな.
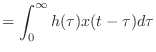 |
(13.53) | |
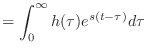 |
(13.54) | |
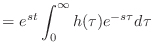 |
(13.55) | |
| (13.56) |
出発点は式 (13.1) の微分方程式だ.
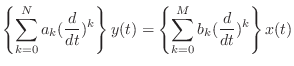 |
(13.1) |
この ![]() ,
,![]() をフーリエ逆変換で置き換えてみよう.
をフーリエ逆変換で置き換えてみよう.
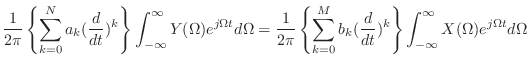 |
(13.57) |
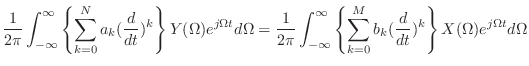 |
(13.58) |
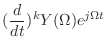 |
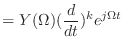 |
(13.59) |
| (13.60) |
![$\displaystyle \frac{1}{2\pi}\int_{-\infty}^{\infty} \left[\left\{\sum_{k = 0}^{...
..._{k = 0}^{M} b_k (j\Omega)^{k} \right\} X(\Omega) \right] e^{j\Omega t} d\Omega$](img1096.png) |
(13.61) |
![$\displaystyle y(t) = {\cal F}^{-1} \left[ \frac{\sum_{k = 0}^{M} b_k (j\Omega)^{k}} {\sum_{k = 0}^{N} a_k (j\Omega)^{k}} X(\Omega) \right]$](img1099.png) |
(13.64) |
何度か話した通り,信号 ![]() をフーリエ変換するってのは,
をフーリエ変換するってのは, ![]() をベクトルとみなして周波数
をベクトルとみなして周波数 ![]() ごとの基底ベクトル
ごとの基底ベクトル
![]() の方向に成分分解することだった.
の方向に成分分解することだった.
![\includegraphics[scale=0.5]{fig_laplace/decomp.eps}](img1100.png)
![\includegraphics[scale=0.5]{fig_laplace/decomp_diff.eps}](img1108.png)
![]() や
や ![]() を各方向に分解してからこの一連の操作をすることを考えると,この操作によってやっぱり各成分の方向は変わらずに伸縮だけすることになる.操作後のベクトルが両辺で一致するということは,操作後の各方向の長さ同士も一致するということだ.これがあらゆる方向
を各方向に分解してからこの一連の操作をすることを考えると,この操作によってやっぱり各成分の方向は変わらずに伸縮だけすることになる.操作後のベクトルが両辺で一致するということは,操作後の各方向の長さ同士も一致するということだ.これがあらゆる方向
![]() についていえる.その関係が代数方程式 (13.62) で表されている.
についていえる.その関係が代数方程式 (13.62) で表されている.
同じ微分方程式を考えて,今度は ![]() ,
,![]() のラプラス変換を
のラプラス変換を ![]() ,
,
![]() と書くことにしよう.
と書くことにしよう.![]() ,
,![]() を逆ラプラス変換で置き換えて同様に考えていくと,
を逆ラプラス変換で置き換えて同様に考えていくと,![]() のところが
のところが
![]() になるだけで後は全く同様の議論ができる.つまり,
になるだけで後は全く同様の議論ができる.つまり,
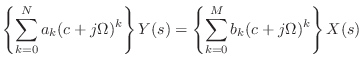 |
(13.65) |
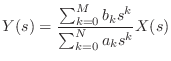 |
(13.67) |
| (13.69) |
| (13.70) |
| (13.71) |
| (13.72) | ||
| (13.73) | ||
| (13.74) |
| (13.75) | ||
| (13.76) | ||
| (13.77) |
![$\displaystyle {\cal L}^{-1}\left[\frac{1}{s + 1} - \frac{1}{s + 2} \right]$](img1132.png) |
(13.78) |
さて,今,ラプラス逆変換で時間領域に戻してもらったわけだが,戻さなくても,部分分数展開できた時点でインパルス応答の挙動はもうわかったようなものだろう?
同じように,「分母 = 0」の解として例えば ![]() が出て来たとすると,インパルス応答は
が出て来たとすると,インパルス応答は ![]() を含むので発散すると判断できるだろう.
を含むので発散すると判断できるだろう.
複素数解が出て来たらどうなる?
![]() が極のとき,インパルス応答が
が極のとき,インパルス応答が ![]() という要素を含むことになる.正確には,分母 = 0 が重解を持つときはちょっと話が違うのだが
その場合も大勢は変わらないので置いておこう.
という要素を含むことになる.正確には,分母 = 0 が重解を持つときはちょっと話が違うのだが
その場合も大勢は変わらないので置いておこう.![]() の実部の正負によって発散/収束が決まるし,虚部によって振動の周波数が決まってくる.
の実部の正負によって発散/収束が決まるし,虚部によって振動の周波数が決まってくる.
![\includegraphics[scale=0.5]{fig_laplace/roc_pole.eps}](img1151.png)
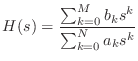 |
(13.68) |
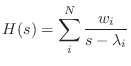 |
(13.79) |
![\includegraphics[scale=0.5]{fig_laplace/sum_hi.eps}](img1161.png)
| (13.80) |
| (13.81) |
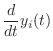 |
(13.82) |
フーリエ変換の場合,どんな信号でも定常的な振動に無理やり分解してしまうので,そういう減衰とか発散のような過渡的な挙動が抽出できないんだな.ラプラス変換ならそれができる.
…あれー,でも別に
![]() って定義しなくても,フーリエ変換のまま考えて
って定義しなくても,フーリエ変換のまま考えて
![]() という変数を導入したとしても,同じことはできるんじゃないかお?
という変数を導入したとしても,同じことはできるんじゃないかお?
結局本質的な役割を果たしたのは,実数 ![]() として,あるいは純虚数
として,あるいは純虚数
![]() として定義されていた周波数という概念を,複素数
として定義されていた周波数という概念を,複素数 ![]() に拡張したことだといえるだろうな.
に拡張したことだといえるだろうな.
以前も強調した通り,こういう風に「信号」と「システム」を同一視できるところが,線形時不変システムの著しい特徴だ.
![\includegraphics[scale=0.5]{fig_laplace/ft_in_s_plane.eps}](img1173.png)
ただし,ラプラス変換は積分範囲を 0 から ![]() に取っているので,変換される時間信号が
に取っているので,変換される時間信号が ![]() で 0 であるようなものでないと一致しないけどな.
で 0 であるようなものでないと一致しないけどな.
![$\displaystyle = {\cal L}[\frac{e^{j\Omega_1 t} + e^{-j\Omega_1 t}}{2}]$](img1179.png) |
(13.83) | |
| (13.84) | ||
| (13.85) |
| (13.86) | ||
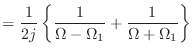 |
(13.87) |
![\includegraphics[scale=0.5]{fig_laplace/ft_sin_u0.eps}](img1185.png)
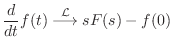 |
(13.88) |
![\includegraphics[scale=0.5]{fig_laplace/lt_f_u0.eps}](img1192.png)
![\includegraphics[scale=0.5]{fig_laplace/lt_diff_f_u0.eps}](img1195.png)
![\includegraphics[scale=0.5]{fig_laplace/u0_lt_diff_f.eps}](img1196.png)
| (13.2) |
| (13.89) | ||
| (13.90) | ||
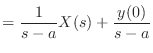 |
(13.91) |
| (13.92) |
というわけで,まとめるか.
swk(at)ic.is.tohoku.ac.jp