: この文書について... : やる夫で学ぶディジタル信号処理 : A. 伝達関数の部分分数展開 目次 アイコンを表示する
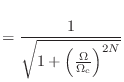 |
(16.20) |
まず前提として,
![]() のインパルス応答
のインパルス応答
![]() は実信号だとする.すると,それをフーリエ変換した
は実信号だとする.すると,それをフーリエ変換した
![]() は振幅が偶関数,位相が奇関数になる.これはわかるな?
は振幅が偶関数,位相が奇関数になる.これはわかるな?
| (B.1) |
| (B.2) | ||
| (B.3) | ||
| (B.4) |
| (B.5) | ||
| (B.6) | ||
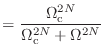 |
(B.7) |
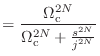 |
(B.8) | |
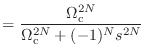 |
(B.9) |
| (B.10) |
| (B.11) | ||
| (B.12) |
| (B.13) |
| (B.14) |
で,![]() が偶数のときは
が偶数のときは
![]() だから,えーと,
だから,えーと,![]() が
が ![]() の奇数倍ってことかお.つまり
の奇数倍ってことかお.つまり
![]() だから,
だから,
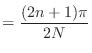 |
(B.15) |
![\includegraphics[scale=0.5]{fig_butterworth/G_poles.eps}](img1898.png)
要求仕様を次のように与えることにする.阻止域に入る最小の周波数を
![]() として,そのときの振幅を
として,そのときの振幅を ![]() とする.
とする.
| (B.16) |
| (B.17) | ||
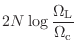 |
(B.18) | |
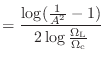 |
(B.19) |
swk(at)ic.is.tohoku.ac.jp