: 3. フーリエ変換 : やる夫で学ぶディジタル信号処理 : 1. フーリエ級数 目次 アイコンを表示する
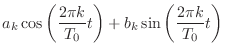 |
(2.1) |
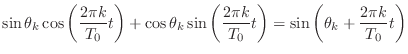 |
(2.2) |
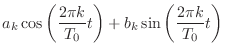 |
(2.3) | |
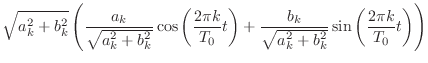 |
(2.4) |
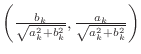 は単位円上の点になるから,
は単位円上の点になるから,
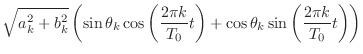 |
(2.5) | |
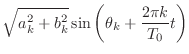 |
(2.6) |
![\includegraphics[scale=0.5]{fig_fs_comp/tan_theta_k.eps}](img128.png)
![\includegraphics[scale=0.5]{fig_fs_comp/sin_cos_sin.eps}](img129.png)
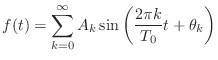 |
(2.7) |
| (2.9) |
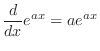 |
(2.10) |
![\includegraphics[scale=0.5]{fig_fs_comp/euler.eps}](img138.png)
| (2.11) |
![\includegraphics[scale=0.5]{fig_fs_comp/euler_rot.eps}](img142.png)
| (2.12) | |
| (2.13) |
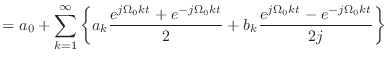 |
(2.16) | |
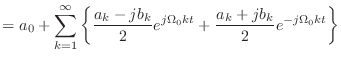 |
(2.17) |
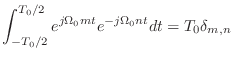 |
(2.20) |
![\includegraphics[scale=0.5]{fig_fs_comp/exp_j_pi_odd_even.eps}](img173.png)
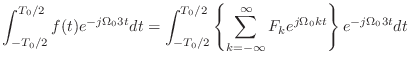 |
(2.26) |
結局,フーリエ係数
![]() は,
は,
以降,![]() をフーリエ級数展開して係数
をフーリエ級数展開して係数 ![]() が得られることを
が得られることを
![\includegraphics[scale=0.5]{fig_fs_comp/axes_re_im_t.eps}](img183.png)
![\includegraphics[scale=0.5]{fig_fs_comp/exp_jomgt.eps}](img184.png)
![\includegraphics[scale=0.5]{fig_fs_comp/exp_jomgt_both.eps}](img186.png)
![\includegraphics[scale=0.5]{fig_fs_comp/pos_neg_freq.eps}](img187.png)
展開したい関数 ![]() が実数値を取るとしよう.するとそれぞれの周波数成分もやっぱり実関数になってくれないと困るわけだ.だから,
が実数値を取るとしよう.するとそれぞれの周波数成分もやっぱり実関数になってくれないと困るわけだ.だから,
![]() と
と
![]() が足し合わされて,さっきと同様に虚数部分が打ち消されるようになっている.そう考えると
が足し合わされて,さっきと同様に虚数部分が打ち消されるようになっている.そう考えると ![]() と
と ![]() がどういう値じゃなくちゃならないかが見えてくるだろ.ちなみに
がどういう値じゃなくちゃならないかが見えてくるだろ.ちなみに ![]() も
も ![]() も一般に複素数だということに注意しとこう.
も一般に複素数だということに注意しとこう.
![\includegraphics[scale=0.5]{fig_fs_comp/spectrum_sinusoid.eps}](img194.png)
次にこれが複素指数関数型のフーリエ級数だ.同じく基本周波数の整数倍の周波数を持つ成分に分解される.ただし,各周波数について,正と負の周波数の組で表される.フーリエ係数は複素数だから,このグラフでは絶対値と偏角にわけてかいてみた.
![\includegraphics[scale=0.5]{fig_fs_comp/spectrum_exp.eps}](img195.png)
こんな風に周波数成分に分解されたものを「スペクトル」とか「周波数スペクトル」とか呼ぶことが多い.特に ![]() のみを考えると「振幅スペクトル」,
のみを考えると「振幅スペクトル」,
![]() のみを考えると位相スペクトルと呼ぶ.
のみを考えると位相スペクトルと呼ぶ.
swk(at)ic.is.tohoku.ac.jp